题目内容
20.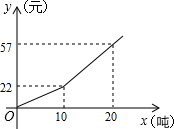 为了节约水资源,自来水公司按分段收费标准收费,如图所示反映的是每月收取水费y(元)与用水量x(吨)之间的函数关系,当每月用水量14吨时,水费是36元.
为了节约水资源,自来水公司按分段收费标准收费,如图所示反映的是每月收取水费y(元)与用水量x(吨)之间的函数关系,当每月用水量14吨时,水费是36元.
分析 设每月收取水费y(元)与用水量x(吨)之间的函数关系式为y=kx+b,观察函数图象,找出点的坐标,分0≤x≤10和10<x利用待定系数法求出y关于x的函数关系式,再代入x=14即可得出结论.
解答 解:设每月收取水费y(元)与用水量x(吨)之间的函数关系式为y=kx+b,
当0≤x≤10时,有$\left\{\begin{array}{l}{0=0}\\{10k+b=22}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=2.2}\\{b=0}\end{array}\right.$,
∴此时y=2.2x;
当10<x时,有$\left\{\begin{array}{l}{10k+b=22}\\{20k+b=57}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=3.5}\\{b=-13}\end{array}\right.$,
∴此时y=3.5x-13.
当x=14时,y=3.5×14-13=36.
故答案为:36.
点评 本题考查了一次函数图象上点的坐标特征以及待定系数法求函数解析式,解题的关键是分段求出y关于x的函数关系式.本题属于基础题,难度不大,解决该题型题目时,观察函数图象找出点的坐标,再结合点的坐标利用待定系数法求出函数解析式是关键.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
20.不等式-2x>3的解集是( )
| A. | $x>-\frac{2}{3}$ | B. | $x<-\frac{2}{3}$ | C. | $x>-\frac{3}{2}$ | D. | $x<-\frac{3}{2}$ |
12.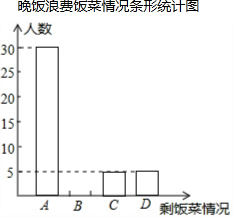 自从2012年12月4日中央公布“八项规定”以来,某中学积极开展“厉行勤俭节约,反对铺张浪费”的活动.为此,校学生会在全校范围内随机抽取了若干名学生就某日晚饭浪费饭菜情况进行调查,调查内容分为四种:A.饭和菜全部吃完;B.有剩饭但菜吃完;C.饭吃完但菜有剩;D.饭和菜都有剩.根据统计结果绘制了如下不完整的统计图表,根据所提供的信息回答下列问题:
自从2012年12月4日中央公布“八项规定”以来,某中学积极开展“厉行勤俭节约,反对铺张浪费”的活动.为此,校学生会在全校范围内随机抽取了若干名学生就某日晚饭浪费饭菜情况进行调查,调查内容分为四种:A.饭和菜全部吃完;B.有剩饭但菜吃完;C.饭吃完但菜有剩;D.饭和菜都有剩.根据统计结果绘制了如下不完整的统计图表,根据所提供的信息回答下列问题:
晚饭浪费饭菜情况统计表
(1)晚饭浪费饭菜情况统计表中的n=10,m=60%.
(2)请把“晚饭浪费饭菜条形统计图”补充完整;
(3)若绘制““晚饭浪费饭菜条形统计图””,调查内容为“饭吃完但菜有剩”所对应的圆心角等于36度
(4)该中学有学生2200名,请估计这餐晚饭中“有饭吃但菜吃完”和“饭吃完但菜有剩”的学生有660人.
 自从2012年12月4日中央公布“八项规定”以来,某中学积极开展“厉行勤俭节约,反对铺张浪费”的活动.为此,校学生会在全校范围内随机抽取了若干名学生就某日晚饭浪费饭菜情况进行调查,调查内容分为四种:A.饭和菜全部吃完;B.有剩饭但菜吃完;C.饭吃完但菜有剩;D.饭和菜都有剩.根据统计结果绘制了如下不完整的统计图表,根据所提供的信息回答下列问题:
自从2012年12月4日中央公布“八项规定”以来,某中学积极开展“厉行勤俭节约,反对铺张浪费”的活动.为此,校学生会在全校范围内随机抽取了若干名学生就某日晚饭浪费饭菜情况进行调查,调查内容分为四种:A.饭和菜全部吃完;B.有剩饭但菜吃完;C.饭吃完但菜有剩;D.饭和菜都有剩.根据统计结果绘制了如下不完整的统计图表,根据所提供的信息回答下列问题:晚饭浪费饭菜情况统计表
| 选项 | 频数 | 频率 |
| A | 30 | m |
| B | n | 20% |
| C | 5 | 10% |
| D | 5 | 10% |
(2)请把“晚饭浪费饭菜条形统计图”补充完整;
(3)若绘制““晚饭浪费饭菜条形统计图””,调查内容为“饭吃完但菜有剩”所对应的圆心角等于36度
(4)该中学有学生2200名,请估计这餐晚饭中“有饭吃但菜吃完”和“饭吃完但菜有剩”的学生有660人.
10.某校为了解本校500名学生的体重情况,从中抽取了50名学生测量体重,下列说法中正确的是( )
| A. | 总体是500名学生 | B. | 样本容量是50 | ||
| C. | 该调查方式是普查 | D. | 个体是50名学生的体重 |