题目内容
5.甲乙两地相距300千米,一辆慢车从甲地出发驶向乙地,45分钟后,一辆快车以每小时比慢车快10千米的速度由乙地出发驶向甲地,两车恰好在甲乙两地中点处相遇,请分别求出两车的速度.分析 设慢车速度为x千米/时,快车的速度为(x+10)千米/时,根据两车同时行驶150千米所用时间之差为45分钟列出方程,求出x的值即可.
解答 解:设慢车速度为x千米/时,快车的速度为(x+10)千米/时,
根据题意可得$\frac{150}{x}$-$\frac{150}{x+10}$=$\frac{3}{4}$,
即x2+10x-2000=0,
解得x1=40或 x2=-50(舍去)
快车速度 为40+10=50千米/时,
答:快车的速度为50千米/时,慢车的速度为40千米/时.
点评 本题主要考查了分式方程的应用,解题的关键是根据两车走相同距离的路程所用时间相差45分钟列出分式方程.

练习册系列答案
相关题目
4.已知a是实数$\sqrt{10}$的整数部分,b是$\sqrt{10}$的小数部分,那么a-b值是( )
| A. | 3+$\sqrt{10}$ | B. | 3-$\sqrt{10}$ | C. | $\sqrt{10}$-3 | D. | 6-$\sqrt{10}$ |
17.不等式|x-1|<1的解集是( )
| A. | x>2 | B. | x<0 | C. | 1<x<2 | D. | 0<x<2 |
14.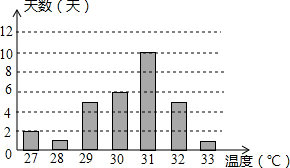 小慧将今年五月深圳每天的最高气温情况绘制成条形统计图,根据图中信息,五月最高气温的众数与中位数分别为( )
小慧将今年五月深圳每天的最高气温情况绘制成条形统计图,根据图中信息,五月最高气温的众数与中位数分别为( )
 小慧将今年五月深圳每天的最高气温情况绘制成条形统计图,根据图中信息,五月最高气温的众数与中位数分别为( )
小慧将今年五月深圳每天的最高气温情况绘制成条形统计图,根据图中信息,五月最高气温的众数与中位数分别为( )| A. | 33,30 | B. | 31,30 | C. | 31,31 | D. | 31,33 |
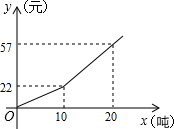 为了节约水资源,自来水公司按分段收费标准收费,如图所示反映的是每月收取水费y(元)与用水量x(吨)之间的函数关系,当每月用水量14吨时,水费是36元.
为了节约水资源,自来水公司按分段收费标准收费,如图所示反映的是每月收取水费y(元)与用水量x(吨)之间的函数关系,当每月用水量14吨时,水费是36元.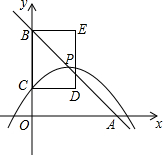 如图,在平面直角坐标系中,直线y=-x+4与x轴、y轴分别交于点A、B.抛物线y=-$\frac{1}{3}{(x-m)^2}$+n的顶点P在直线y=-x+4上,与y轴交于点C(点P、C不与点B重合),以BC为边作矩形BCDE,且CD=2,点P、D在y轴的同侧.
如图,在平面直角坐标系中,直线y=-x+4与x轴、y轴分别交于点A、B.抛物线y=-$\frac{1}{3}{(x-m)^2}$+n的顶点P在直线y=-x+4上,与y轴交于点C(点P、C不与点B重合),以BC为边作矩形BCDE,且CD=2,点P、D在y轴的同侧. 2015年8月17日大河网报道,大学生身体素质不如中学生,王老师为了解该校八年级500名学生的体能情况,随机抽取了50名学生,测试了1分钟仰卧起坐的次数,并将数据绘制成如图所示的频数分布直方图(注:15~20包括15,不包括20,下同).已知第1组的频数为2,第2组的频率为20%,则这次测试中合格(1分钟仰卧起坐的次数大于等于25)的学生有(
2015年8月17日大河网报道,大学生身体素质不如中学生,王老师为了解该校八年级500名学生的体能情况,随机抽取了50名学生,测试了1分钟仰卧起坐的次数,并将数据绘制成如图所示的频数分布直方图(注:15~20包括15,不包括20,下同).已知第1组的频数为2,第2组的频率为20%,则这次测试中合格(1分钟仰卧起坐的次数大于等于25)的学生有(