题目内容
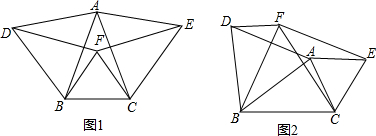
17.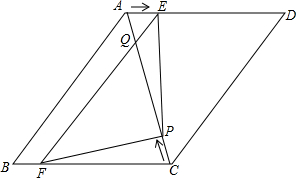 如图,在?ABCD中,AB=6cm,AD=AC=5cm,点P由C出发沿CA方向匀速运动,速度为1cm/s;同时,线段EF由AB出发沿AD方向匀速运动,速度为1cm/s,交AC于Q,连接PE、PF,若运动时间为t(s)(0<t<2.5).解答下列问题:
如图,在?ABCD中,AB=6cm,AD=AC=5cm,点P由C出发沿CA方向匀速运动,速度为1cm/s;同时,线段EF由AB出发沿AD方向匀速运动,速度为1cm/s,交AC于Q,连接PE、PF,若运动时间为t(s)(0<t<2.5).解答下列问题:(1)当t为何值时,PE∥CD?
(2)试判断△PEF形状,并说明理由;
(3)请求五边形ABEFPE的面积;
(4)求△PFC的面积s与t的函数关系式:并确定当t为何值时,s有最大值?最大值是多少?
分析 (1)首先用t表示出AE、CP、AP的长,若PE∥CD,那么△APE∽△ACD,根据相似三角形所得比例线段即可求得此时t的值.
(2)由于AD=AC,且QE∥CD,所以△AQE也是等腰三角形,即AQ=AE,由P、Q的速度可知:CP=AE=AQ,进而可求得CQ=AP,同理可证得△CFQ也是等腰三角形,即CF=CQ,由此得CF=AP,已求得AE=PC,而∠DAC=∠FCP,由此可证得△FCP≌△PAE,即可证得PF=PE,即△PEF是等腰三角形.
(3)由(2)的全等三角形知:△AEP、△EPC的面积相等,因此五边形的面积可转化为△ABC的面积,所以五边形的面积是个定值;
(4)由(1)的相似三角形,易求得QE的表达式,分别过C、P作AB、EF的垂线CG、PH,交AB于G,交EF于H,根据等腰三角形三线合一的性质,易求得AG、BG的值,进而可求得∠ACG(即∠EPH)的余弦值,即可根据PQ的长表示出QE边上的高PH的值,由三角形的面积公式,可得关于△PQE的面积和t的函数关系式,根据函数的性质即可得到△PQE的最大面积,从而求得其面积的取值范围.
解答 解:(1)由题意知AE=BF=CP=t,AP=5-t,
在?ABCD中,AD=BC=AC=5,AB=EF=CD=6,
当PE∥CD时,△APE∽△ACD,
∴$\frac{t}{5}=\frac{5-t}{5}$,
∴t=2.5;
(2)是等腰三角形,
∵在?ABCD中,AD=BC=AC=5,AB=EF=CD=6,
∴∠CAB=∠CBA,
∵AB∥EF,∴∠CQF=∠CAB,∠CFQ=∠CBA,
∴∠CFQ=∠CQF,
∴CF=CQ,
∴AQ=BF=AE,
∴AP=CQ=CF,
∵AD∥BC,
∴∠PAE=∠FCP,
∴△PAE≌△FCP(SAS),
∴PE=PF;
(3))由(2)的全等三角形知:S△AEP=S△PCF,即S五边形BFPEA=S△ABC;
过C作CG⊥AB于G,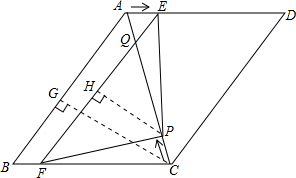
等腰△ACB中,AG=BG=3,AC=BC=5,则CG=4,
∴S五边形BFPEA=S△ABC=$\frac{1}{2}$×6×4=12;
(4)∵QE∥AB∥CD,
∴△AQE∽△ACD,
∴$\frac{QE}{CD}=\frac{AE}{AD}$,即$\frac{QE}{6}$=$\frac{t}{5}$,QE=$\frac{6t}{5}$,
S△ACD=S△ABC=$\frac{1}{2}$•AB•CG=$\frac{1}{2}×6×4$=12,
∴S△AQE=${(\frac{AE}{AD})}^{2}{•S}_{△ACD}$=$\frac{{t}^{2}}{25}$×12=$\frac{12}{25}$t2
过P作PH⊥EF于H,由(3)易得:cos∠APH=cos∠ACG=$\frac{4}{5}$,
故PH=$\frac{4}{5}$PQ=$\frac{4}{5}$(5-2t);
设△PEQ的面积为y,则y=$\frac{1}{2}$$•\frac{6}{5}t•\frac{4}{5}(5-2t)$=$-\frac{24}{25}{t}^{2}+\frac{12}{5}t$,
∴S△PFC=S△EPA=$\frac{12}{25}$t2+($-\frac{24}{25}$t2$+\frac{12}{5}$t)=$-\frac{12}{25}$t2$+\frac{12}{5}$t=$-\frac{12}{25}$${(t-\frac{1}{2})}^{2}$$+\frac{3}{25}$
∴当t=$\frac{1}{2}$时,S△PFC最大=$\frac{3}{25}$,
∴0<S△PFC≤$\frac{3}{25}$.
点评 本题主要考查了平行四边形的性质、相似三角形的判定和性质、全等三角形的性质、等腰三角形的性质以及二次函数最值,数形结合,利用二次函数求最值是解答此题的关键.

| A. | 2a2-a2=2 | B. | (-a)6÷(-a)2=(-a)3 | C. | (a+b)2=a2+b2 | D. | 2a-1=$\frac{2}{a}$ |
| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{16}{5}$ | D. | $\frac{9}{5}$ |
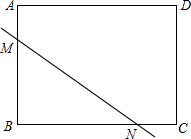 在矩形ABCD中,AB=6,AD=8,把矩形ABCD沿直线MN翻折,点B落在边AD上的E点处.若AE=2AM,那么EN的长等于3$\sqrt{5}$.
在矩形ABCD中,AB=6,AD=8,把矩形ABCD沿直线MN翻折,点B落在边AD上的E点处.若AE=2AM,那么EN的长等于3$\sqrt{5}$.