题目内容
5.现有一组有规律排列的数:1、-1、$\sqrt{2}$、-$\sqrt{2}$、$\sqrt{3}$、-$\sqrt{3}$、1、-1、$\sqrt{2}$、-$\sqrt{2}$、$\sqrt{3}$、-$\sqrt{3}$、…其中,1、-1、$\sqrt{2}$、-$\sqrt{2}$、$\sqrt{3}$、-$\sqrt{3}$这六个数按此规律重复出现.问:(1)第50个数是什么数?
(2)把从第1个数开始的前2015个数相加,结果是多少?
(3)从第1个数起,把连续若干个数的平方加起来,如果和为520,则共有多少个数的平方相加?
分析 (1)首先根据这列数的排列规律,可得每6个数一个循环:1、-1、$\sqrt{2}$、-$\sqrt{2}$、$\sqrt{3}$、-$\sqrt{3}$;然后用50除以6,根据余数的情况判断出第50个数是什么数即可;
(2)首先用2015除以6,求出一共有多少个循环,以及剩下的数是多少;然后用循环的个数乘以1+(-1)+$\sqrt{2}$+(-$\sqrt{2}$)+($\sqrt{3}$)+(-$\sqrt{3}$),再加上剩下的数,求出把从第1个数开始的前2015个数相加,结果是多少即可;
(3)首先求出1、-1、$\sqrt{2}$、-$\sqrt{2}$、$\sqrt{3}$、-$\sqrt{3}$六个数的平方和是多少;然后用520除以六个数的平方和,根据商和余数的情况,判断出一共有多少个数的平方相加即可.
解答 解:(1)这列数每6个数一个循环:1、-1、$\sqrt{2}$、-$\sqrt{2}$、$\sqrt{3}$、-$\sqrt{3}$;
∵50÷6=8…2,
∴第50个数是-1.
(2)∵2015÷6=335…5,1+(-1)+$\sqrt{2}$+(-$\sqrt{2}$)+($\sqrt{3}$)+(-$\sqrt{3}$)=0,
$1+(-1)+\sqrt{2}+(-\sqrt{2})+\sqrt{3}=\sqrt{3}$,
∴从第1个数开始的前2015个数的和是:
335×0+$\sqrt{3}$=$\sqrt{3}$.
(3)∵${1}^{2}{+(-1)}^{2}{+(\sqrt{2})}^{2}{+(-\sqrt{2})}^{2}$${+(\sqrt{3})}^{2}{+(-\sqrt{3})}^{2}$=12,
520÷12=43…4,而且${1}^{2}{+(-1)}^{2}{+(\sqrt{2})}^{2}=4$,
∴43×6+3=261,
即共有261个数的平方相加.
点评 此题主要考查了探寻数列规律问题,注意观察总结规律,并能正确的应用规律,解答此题的关键是判断出:这列数每6个数一个循环:1、-1、$\sqrt{2}$、-$\sqrt{2}$、$\sqrt{3}$、-$\sqrt{3}$,而且每个循环的6个数的和是0.

 习题精选系列答案
习题精选系列答案| A. | 27$\sqrt{2}$海里 | B. | 18$\sqrt{3}$海里 | C. | 27$\sqrt{3}$海里 | D. | 18$\sqrt{2}$海里 |
| A. | 36 | B. | 40 | C. | 45 | D. | 46 |
| A. | 若x>y,则x2>y2 | |
| B. | 若(x1,y1)、(x2,y2)是函数$y=\frac{2}{x}$图象上的两点,且x1<x2,则y1>y2 | |
| C. | 有两角及一边对应相等的两个三角形全等 | |
| D. | 对角线互相垂直的平行四边形是正方形 |
 如图是一架婴儿车,其中AB∥CD,∠AFG=130°,∠D=40°,那么∠AEF=( )
如图是一架婴儿车,其中AB∥CD,∠AFG=130°,∠D=40°,那么∠AEF=( )| A. | 80° | B. | 90° | C. | 100° | D. | 102° |
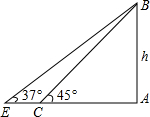 如图,数学课外活动小组测电视塔AB的高度,他们在点C处测得塔顶B的仰角为45°,自C点沿AC方向前进40米到达点E,在点E处测得B的仰角为37°(A、C、E三点在一条直线上).求电视塔的高度h.(结果精确到0.1米,参考数据:sin37°≈$\frac{3}{5}$,cos37°≈$\frac{4}{5}$,tan37°≈$\frac{3}{4}$)
如图,数学课外活动小组测电视塔AB的高度,他们在点C处测得塔顶B的仰角为45°,自C点沿AC方向前进40米到达点E,在点E处测得B的仰角为37°(A、C、E三点在一条直线上).求电视塔的高度h.(结果精确到0.1米,参考数据:sin37°≈$\frac{3}{5}$,cos37°≈$\frac{4}{5}$,tan37°≈$\frac{3}{4}$)