题目内容
15.一艘轮船以18海里/时沿北偏东60°的方向航行,上午九时,测得小岛A在正东方向,3小时后,看见小岛在南偏东30°方向上,此时船与小岛的距离为( )| A. | 27$\sqrt{2}$海里 | B. | 18$\sqrt{3}$海里 | C. | 27$\sqrt{3}$海里 | D. | 18$\sqrt{2}$海里 |
分析 作高线BD,在直角△ABD中,根据正弦函数即可求得BD,在直角△BCD中,利用余弦函数即可求得BC的长度.
解答 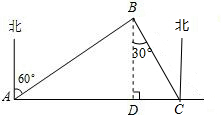 解:解:如图,过B点作BD⊥AC于D.
解:解:如图,过B点作BD⊥AC于D.
∵∠DAB=90°-60°=30°.AB=18×3=54,
在Rt△ABD中,BD=AB•sin∠DAB=54×$\frac{1}{2}$=27,
在Rt△BDC中,∵∠CBD=30°,
∴BC=$\frac{BD}{cos∠CBD}$=$\frac{27}{cos30°}$=$\frac{27}{\frac{\sqrt{3}}{2}}$=18$\sqrt{3}$(海里).
故选B.
点评 本题考查了解直角三角形的应用-方向角问题,解一般三角形,求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5. 如图,将长为2,宽为1的矩形纸片分割成n个三角形后,拼成面积为2的正方形,则n可能是( )
如图,将长为2,宽为1的矩形纸片分割成n个三角形后,拼成面积为2的正方形,则n可能是( )
 如图,将长为2,宽为1的矩形纸片分割成n个三角形后,拼成面积为2的正方形,则n可能是( )
如图,将长为2,宽为1的矩形纸片分割成n个三角形后,拼成面积为2的正方形,则n可能是( )| A. | 2或4 | B. | 2或3 | C. | 3或5 | D. | 2或5 |
4.二次函数y=-2(x+1)2-3图象的顶点坐标为( )
| A. | (1,3) | B. | (1,-3) | C. | (-1,3) | D. | (-1,-3) |
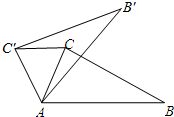 如图,在△ABC中,∠CAB=65°,在同一平面内,将△ABC绕点A逆时针旋转到△AB′C′的位置,使得C′C∥AB,则∠B′AB等于50°.
如图,在△ABC中,∠CAB=65°,在同一平面内,将△ABC绕点A逆时针旋转到△AB′C′的位置,使得C′C∥AB,则∠B′AB等于50°.