题目内容
10.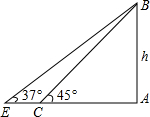 如图,数学课外活动小组测电视塔AB的高度,他们在点C处测得塔顶B的仰角为45°,自C点沿AC方向前进40米到达点E,在点E处测得B的仰角为37°(A、C、E三点在一条直线上).求电视塔的高度h.(结果精确到0.1米,参考数据:sin37°≈$\frac{3}{5}$,cos37°≈$\frac{4}{5}$,tan37°≈$\frac{3}{4}$)
如图,数学课外活动小组测电视塔AB的高度,他们在点C处测得塔顶B的仰角为45°,自C点沿AC方向前进40米到达点E,在点E处测得B的仰角为37°(A、C、E三点在一条直线上).求电视塔的高度h.(结果精确到0.1米,参考数据:sin37°≈$\frac{3}{5}$,cos37°≈$\frac{4}{5}$,tan37°≈$\frac{3}{4}$)
分析 在Rt△ACB中,得到AC=AB=h,在Rt△AEB中,根据$\frac{h}{40+h}$=tan37°,求出h即可.
解答 解:在Rt△ACB中,AC=AB=h,
在Rt△AEB中,$\frac{h}{40+h}$=tan37°,
解得,$\frac{h}{40+h}$≈$\frac{3}{4}$,
即h≈120.0米.
点评 本题考查了解直角三角形的应用--仰角俯角问题,要求学生能借助仰角构造直角三角形并解直角三角形.

练习册系列答案
相关题目
2.下列计算正确的是( )
| A. | a+a2=2a2 | B. | (-a-b)(a-b)=b2-a2 | C. | a2×a3=a6 | D. | (-3a2bc3)2=6a4b6 |
20.下列计算正确的是( )
| A. | (ab)2=a2b2 | B. | (a+b)2=a2+b2 | C. | (a4)2=a6 | D. | a6÷a2=a3 |
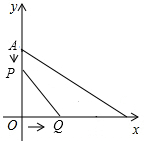 如图,在平面直角坐标系中,已知点A(0,6),B(8,0).点P从A点出发,以每秒1个单位的速度沿AO运动;同时,点Q从O出发,以每秒2个单位的速度沿OB运动,当Q点到达B点时,P、Q两点同时停止运动.
如图,在平面直角坐标系中,已知点A(0,6),B(8,0).点P从A点出发,以每秒1个单位的速度沿AO运动;同时,点Q从O出发,以每秒2个单位的速度沿OB运动,当Q点到达B点时,P、Q两点同时停止运动.