��Ŀ����
14����1����ͼ��������������y=$\frac{k}{x}$��x��0��ͼ��������һ��P��x��y�����ֱ���x����y�������ߣ����߶ηֱ�ΪPA��PB��֤����S����OAPB=k��S��OAP=$\frac{1}{2}$k��S��OPB=$\frac{1}{2}$k����2����ͼ������������y=$\frac{k}{x}$��x��0����ͼ������OABC�Խ��ߵĽ���M���ֱ���AB��BC���ڵ�D��E�����ı���ODBE�����Ϊ9����k��ֵ��

���� ��1����P��x��y���ڷ���������y=$\frac{k}{x}$��x��0��ͼ���ϣ��õ�xy=k�����ɾ��ε������ʽ�������ε������ʽ��ã�
��2������ɴӷ���������ͼ���ϵĵ�E��M��D���֣��ֱ��ҳ���OCE����OAD������OABC�������|k|�Ĺ�ϵ���г���ʽ���kֵ��
��� �⣺��1���ߵ�P��x��y���ڷ���������y=$\frac{k}{x}$��x��0��ͼ���ϣ�
��xy=k��
��PA��x�ᣬPB��y�ᣬ
���ı���OAPB�Ǿ��Σ�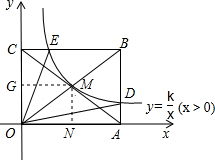
��PB=OA=x��OB=PA=y��
��S����OAPB=OA•OB=xy=k��S��OAP=$\frac{1}{2}$OA•AP=$\frac{1}{2}$xy=$\frac{1}{2}$k��S��OPB=$\frac{1}{2}$OB•PB=$\frac{1}{2}$xy=$\frac{1}{2}$k��
��2����ͼ��������ã�E��M��Dλ�ڷ���������ͼ���ϣ���S��OCE=$\frac{|k|}{2}$��S��OAD=$\frac{|k|}{2}$��
����M��MG��y���ڵ�G����MN��x���ڵ�N����S��ONMG=|k|��
�֡�MΪ����ABCO�Խ��ߵĽ��㣬
��S����ABCO=4S��ONMG=4|k|��
���ں���ͼ���ڵ�һ���ޣ�k��0����$\frac{k}{2}$+$\frac{k}{2}$+9=4k��
��ã�k=3��
���� ���⿼�鷴��������ϵ��k�ļ������壬��˫�����ϵ�����һ��ֱ������������������ߣ���������Χ�ɵľ�������͵���|k|����֪ʶ�����п�����Ҫ���㣬�������������ν�ϵ�˼�룬��������һ��Ҫ��ȷ����k�ļ������壮

| A�� | ��1��3�� | B�� | ��1��-3�� | C�� | ��-1��3�� | D�� | ��-1��-3�� |
| A�� | a+a2=2a2 | B�� | ��-a-b����a-b��=b2-a2 | C�� | a2��a3=a6 | D�� | ��-3a2bc3��2=6a4b6 |
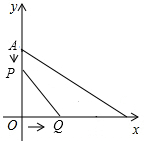 ��ͼ����ƽ��ֱ������ϵ�У���֪��A��0��6����B��8��0������P��A���������ÿ��1����λ���ٶ���AO�˶���ͬʱ����Q��O��������ÿ��2����λ���ٶ���OB�˶�����Q�㵽��B��ʱ��P��Q����ͬʱֹͣ�˶���
��ͼ����ƽ��ֱ������ϵ�У���֪��A��0��6����B��8��0������P��A���������ÿ��1����λ���ٶ���AO�˶���ͬʱ����Q��O��������ÿ��2����λ���ٶ���OB�˶�����Q�㵽��B��ʱ��P��Q����ͬʱֹͣ�˶���