题目内容
7.如果A、B、C三点在同一直线上,且线段AB=6cm,BC=4cm,若M,N分别为AB,BC的中点,那么M,N两点之间的距离为( )| A. | 5 cm | B. | 1 cm | C. | 5或1 cm | D. | 无法确定 |
分析 分点B在线段AC上和点C在线段AB上两种情况,根据线段中点的性质进行计算即可.
解答  解:如图1,当点B在线段AC上时,
解:如图1,当点B在线段AC上时,
∵AB=6cm,BC=4cm,M,N分别为AB,BC的中点,
∴MB=$\frac{1}{2}$AB=3,BN=$\frac{1}{2}$BC=2,
∴MN=MB+NB=5cm,
如图2,当点C在线段AB上时,
∵AB=6cm,BC=4cm,M,N分别为AB,BC的中点,
∴MB=$\frac{1}{2}$AB=3,BN=$\frac{1}{2}$BC=2,
∴MN=MB-NB=1cm,
故选C.
点评 本题考查的是两点间的距离,掌握线段中点的性质、灵活运用数形结合思想、分情况讨论思想是解题的关键.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
15.甲、乙两个仓库要向A,B两地调运小麦,已知甲库可以调出80吨,乙库可以调出40吨,A地需要小麦50吨,B地需要70吨.甲,乙两库运往A,B两地的费用如下表:
(1)设甲库运往A地x吨,求总运费y(单位:元)与x之间的函数表达式;
(2)哪种方案总运费最省?并求最省的运费.
| A地(元/吨) | B地(元/吨) | |
| 甲库 | 10 | 40 |
| 乙库 | 20 | 30 |
(2)哪种方案总运费最省?并求最省的运费.
2.已知a,b,c满足$\frac{a}{2}$=$\frac{b-c}{3}$=$\frac{a+c}{5}$,则$\frac{a+c}{2a+b}$的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | 1 | D. | 2 |
16.化简$\frac{{a}^{2}-2ab}{a-b}$-$\frac{{b}^{2}}{b-a}$的结果是( )
| A. | a+b | B. | $\frac{1}{a-b}$ | C. | $\frac{{a}^{2}-2ab-{b}^{2}}{a-b}$ | D. | a-b |
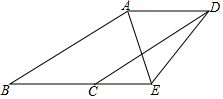 已知如图,∠ABC=∠ADC,AB∥CD,AE平分∠BAD,当∠ADC:∠CDE=3:2,且∠AED=60°时,求∠BED的度数为$\frac{960}{7}$度.
已知如图,∠ABC=∠ADC,AB∥CD,AE平分∠BAD,当∠ADC:∠CDE=3:2,且∠AED=60°时,求∠BED的度数为$\frac{960}{7}$度.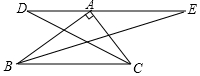 如图,在△ABC中,∠BAC=90°,AC=6,BC=10,过点A的直线DE∥BC,∠ABC与∠ACB的平分线分别交DE于E,D,求DE的长.
如图,在△ABC中,∠BAC=90°,AC=6,BC=10,过点A的直线DE∥BC,∠ABC与∠ACB的平分线分别交DE于E,D,求DE的长.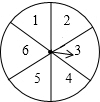 转盘被划分成六个相同大小的扇形,并分别标上1,2,3,4,5,6这六个数字,指针停在每个扇形的可能性相等.四位同学各自发表了下述见解:
转盘被划分成六个相同大小的扇形,并分别标上1,2,3,4,5,6这六个数字,指针停在每个扇形的可能性相等.四位同学各自发表了下述见解: