题目内容
2.已知a,b,c满足$\frac{a}{2}$=$\frac{b-c}{3}$=$\frac{a+c}{5}$,则$\frac{a+c}{2a+b}$的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | 1 | D. | 2 |
分析 设$\frac{a}{2}$=$\frac{b-c}{3}$=$\frac{a+c}{5}$=k,则a=2k,b-c=3k,a+c=5k,然后再求得2a+b=10k,最后代入求解即可.
解答 解:设$\frac{a}{2}$=$\frac{b-c}{3}$=$\frac{a+c}{5}$=k,则a=2k①,b-c=3k②,a+c=5k③.
①+②+③得:2a+b=10k.
∴$\frac{a+c}{2a+b}$=$\frac{5k}{10k}$=$\frac{1}{2}$.
故选:A.
点评 本题主要考查的是求分式的值,求得a+c=5k,2a+b=10k是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17. 为了解国家提倡的“阳光体育运动”的实施情况,将某校中的40名学生一周的体育锻炼时间绘制成了如图所示的条形统计图,根据统计图提供的数据,该校40名同学一周参加体育锻炼时间的众数与中位数分别是( )
为了解国家提倡的“阳光体育运动”的实施情况,将某校中的40名学生一周的体育锻炼时间绘制成了如图所示的条形统计图,根据统计图提供的数据,该校40名同学一周参加体育锻炼时间的众数与中位数分别是( )
 为了解国家提倡的“阳光体育运动”的实施情况,将某校中的40名学生一周的体育锻炼时间绘制成了如图所示的条形统计图,根据统计图提供的数据,该校40名同学一周参加体育锻炼时间的众数与中位数分别是( )
为了解国家提倡的“阳光体育运动”的实施情况,将某校中的40名学生一周的体育锻炼时间绘制成了如图所示的条形统计图,根据统计图提供的数据,该校40名同学一周参加体育锻炼时间的众数与中位数分别是( )| A. | 8,8 | B. | 8,9 | C. | 9,8 | D. | 10,9 |
7.如果A、B、C三点在同一直线上,且线段AB=6cm,BC=4cm,若M,N分别为AB,BC的中点,那么M,N两点之间的距离为( )
| A. | 5 cm | B. | 1 cm | C. | 5或1 cm | D. | 无法确定 |
14.下列各数中,最大的数是( )
| A. | -$\frac{1}{2}$ | B. | (-$\frac{1}{2}$)2 | C. | (-$\frac{1}{2}$)3 | D. | (-$\frac{1}{2}$)4 |
12.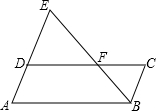 如图,点F是?ABCD的边CD上一点,直线BF交AD的延长线于点E,则下列结论错误的是( )
如图,点F是?ABCD的边CD上一点,直线BF交AD的延长线于点E,则下列结论错误的是( )
 如图,点F是?ABCD的边CD上一点,直线BF交AD的延长线于点E,则下列结论错误的是( )
如图,点F是?ABCD的边CD上一点,直线BF交AD的延长线于点E,则下列结论错误的是( )| A. | $\frac{ED}{EA}$=$\frac{DF}{AB}$ | B. | $\frac{DE}{CB}$=$\frac{EF}{FB}$ | C. | $\frac{BF}{BE}$=$\frac{BC}{AE}$ | D. | $\frac{BC}{DE}$=$\frac{BF}{BE}$ |
 某学校要了解学生上学交通情况,选取七年级全体学生进行调查,根据调查结果,画出扇形统计图(如图),图中“公交车”对应的扇形圆心角为60°,“自行车”对应的扇形圆心角为120°,已知七年级乘公交车上学的人数为50人.
某学校要了解学生上学交通情况,选取七年级全体学生进行调查,根据调查结果,画出扇形统计图(如图),图中“公交车”对应的扇形圆心角为60°,“自行车”对应的扇形圆心角为120°,已知七年级乘公交车上学的人数为50人. 如图,C是线段AB的中点,点D在CB上,且AD=6.5,BD=1.5,则线段CD长为2.5.
如图,C是线段AB的中点,点D在CB上,且AD=6.5,BD=1.5,则线段CD长为2.5.