题目内容
18.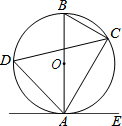 如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠EAC=∠D=60°.
如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠EAC=∠D=60°.(1)求证:AE是⊙O的切线;
(2)当BC=6时,求劣弧AC的长.
分析 (1)由AB是⊙O的直径,根据半圆(或直径)所对的圆周角是直角,即可得∠ACB=90°,又由∠BAC=30°,易求得∠BAE=90°,则可得AE是⊙O的切线;
(2)首先连接OC,易得△OBC是等边三角形,则可得∠AOC=120°,由弧长公式,即可求得劣弧AC的长.
解答 解:(1)∵AB是⊙O的直径,
∴∠ACB=90°.
∴∠BAC=30°,
∴∠BAE=∠BAC+∠EAC=30°+60°=90°,
即BA⊥AE,
∴AE是⊙O的切线;
(2)如图,连接OC,
∵∠B=∠D=60°,OB=OC,
∴△BCO是等边三角形,
∴∠BOC=60°,
∴∠AOC=120°,AB=2BC=12,
∴AO=6,
∴劣弧AC的长为$\frac{120•π•6}{360}$=2π.
点评 此题考查了切线的判定、圆周角定理以及弧长公式等知识.此题难度适中,注意数形结合思想的应用,注意辅助线的作法.

练习册系列答案
相关题目
8.已知⊙O的半径为5,点P在⊙O内,且PO=3,则过点P且弦长为整数的弦有( )条.
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
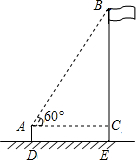 某校初三课外活动小组为了测得学校旗杆的高度,他们在离旗杆6米的D处,用高为2米的仪器测得旗杆顶部B处的仰角为60°,则旗杆的高度为2+6$\sqrt{3}$ 米 (结果保留根号)
某校初三课外活动小组为了测得学校旗杆的高度,他们在离旗杆6米的D处,用高为2米的仪器测得旗杆顶部B处的仰角为60°,则旗杆的高度为2+6$\sqrt{3}$ 米 (结果保留根号)