题目内容
13.已知直线l与直线y=2x+4的交点P的横坐标为3,与直线y=-x-11的交点Q的纵坐标为-8,求直线l的函数关系式.分析 要求直线l对应的函数解析式只要求出经过的两个点的坐标即可.即求直线y=2x+4中横坐标为3,和直线y=-x-11的纵坐标为-8的点,运用待定系数法就可以求出解析式.
解答 解:在直线y=2x+4中,
令x=3,解得y=10,
P点坐标为(3,10),
在y=-x-11中,
令y=-8,解得x=-3,
Q点坐标为(-3,-8),
则直线l经过点P(3,10),Q(-3,-8).
设直线l的解析式是y=kx+b,
根据题意,得$\left\{\begin{array}{l}{3k+b=10}\\{-3k+b=-8}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=3}\\{b=1}\end{array}\right.$.
故直线l对应的函数解析式是:y=3x+1.
点评 此题考查了两条直线相交的问题,用待定系数法求一次函数的解析式.解决本题的关键是求出直线l经过的两个点的坐标,然后利用一次函数的特点,来列出方程组,求出未知数,写出解析式.

练习册系列答案
相关题目
3.“从一布袋中随机地摸出一枚围棋棋子,恰是黑色的概率为$\frac{2}{5}$”的意思是( )
| A. | 摸5次一定能摸到2枚黑子 | |
| B. | 摸5次一定有3次摸到白子 | |
| C. | 摸若干次,平均每5次有2次摸到黑子 | |
| D. | 袋中一定有2枚黑子,3枚白子 |
5.下列各式合并同类项正确的是( )
| A. | x+2x=3x2 | B. | 2m+3n=5mn | C. | 5a4-2a2=3a2 | D. | 3x2y-2yx2=x2y |
2.点A(3,y1)和点B (2,y2)都在直线y=-2x+3上,则y1和y2的大小关系是( )
| A. | y1>y2 | B. | y1<y2 | C. | y1=y2 | D. | 不能确定 |
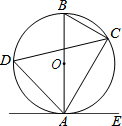 如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠EAC=∠D=60°.
如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠EAC=∠D=60°.