题目内容
19．等腰三角形两边长分别是2和5，则它的周长为（ ）| A． | 12 | B． | 9 | C． | 12或9 | D． | 以上都不对 |
分析 求等腰三角形的周长，即是确定等腰三角形的腰与底的长求周长；题目给出等腰三角形有两条边长为2和5，而没有明确腰、底分别是多少，所以要进行讨论，还要应用三角形的三边关系验证能否组成三角形．
解答 解：（1）若2为腰长，5为底边长，
由于2+2＜5，则三角形不存在；
（2）若5为腰长，则符合三角形的两边之和大于第三边．
所以这个三角形的周长为5+5+2=12．
故选A．
点评 本题考查了等腰三角形的性质和三角形的三边关系；题目从边的方面考查三角形，涉及分类讨论的思想方法．求三角形的周长，不能盲目地将三边长相加起来，而应养成检验三边长能否组成三角形的好习惯，把不符合题意的舍去．
练习册系列答案
相关题目
如图，在梯形ABCD中，AD∥BC，∠ADC=135°，AB+BC=24，AB⊥BC，梯形ABCD的面积为42m2，求AB、BC的大小．
10．下列命题中，正确的是（ ）
| A． | 过一点有且只有一条直线与已知直线垂直 | |
| B． | 过一点有且只有一条直线与已知直线平行 | |
| C． | 垂直于同一直线的两条直线平行 | |
| D． | 平行于同一直线的两条直线平行 |
如图，在平行四边形ABCD中，AM⊥BD于M，CN⊥BD于N，连接CM、AN
11．已知a，b，c为有理数，且a＜b，则下列不等式中正确的是（ ）
| A． | $\frac{a}{c}$＜$\frac{b}{c}$ | B． | ac＜bc | C． | a-c＞b-c | D． | a+c＜b+c |
8．
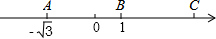如图，在数轴上，点A与点C到点B的距离相等，A，B两点所对应的实数分别是-$\sqrt{3}$和1，则点C对应的实数是（ ）
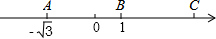如图，在数轴上，点A与点C到点B的距离相等，A，B两点所对应的实数分别是-$\sqrt{3}$和1，则点C对应的实数是（ ）| A． | 1+$\sqrt{3}$ | B． | 2+$\sqrt{3}$ | C． | 2$\sqrt{3}$-1 | D． | 2$\sqrt{3}$+1 |