题目内容
1. 如图,已知在△ABC中,AD平分∠BAC,按如下步骤作图:第一步,分别以点A、D为圆心,大于$\frac{1}{2}$AD的长为半径在AD两侧作弧,交于M、N两点;第二步,连结MN,分别交AB、AC于点E、F;第三步,连结DE、DF.若BD=6,AF=5,CD=3,则BE的长是( )
如图,已知在△ABC中,AD平分∠BAC,按如下步骤作图:第一步,分别以点A、D为圆心,大于$\frac{1}{2}$AD的长为半径在AD两侧作弧,交于M、N两点;第二步,连结MN,分别交AB、AC于点E、F;第三步,连结DE、DF.若BD=6,AF=5,CD=3,则BE的长是( )| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
分析 根据作法可知MN是线段AD的垂直平分线,故可得出四边形AEDF是菱形,再由DE∥AC可得出△BDE∽△BCA,由相似三角形的对应边成比例即可得出结论.
解答 解:∵MN是线段AD的垂直平分线,
∴四边形AEDF是菱形.
∵DE∥AC,
∴△BDE∽△BCA,
∴$\frac{DB}{DC}$=$\frac{BE}{AE}$.
∵BD=6,AE=5,CD=3,
∴$\frac{6}{3}$=$\frac{BE}{5}$,解得BE=10.
点评 本题考查的是作图-基本作图,熟知线段垂直平分线的作法是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.下列二次根式中,不能与$\sqrt{6}$合并的是( )
| A. | $\sqrt{\frac{2}{3}}$ | B. | $\sqrt{24}$ | C. | $\sqrt{1.5}$ | D. | $\sqrt{1.2}$ |
9.下列长度的三条线段中,能组成三角形的是( )
| A. | 3cm,5cm,8cm | B. | 8cm,8cm,18cm | ||
| C. | 0.1cm,0.1cm,0.1cm | D. | 3cm,40cm,8cm |
16.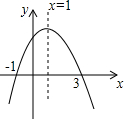 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:
①abc<0
②2a+b=0
③当x=-1或x=3时,函数y的值都等于0.
④4a+2b+c<0
其中正确结论的个数是( )
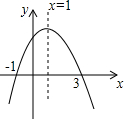 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:①abc<0
②2a+b=0
③当x=-1或x=3时,函数y的值都等于0.
④4a+2b+c<0
其中正确结论的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
10.已知(-3,y1),(0,y2),(3,y3)是抛物线y=-3x2+6x-k上的点,则( )
| A. | y1<y2<y3 | B. | y1<y3<y2 | C. | y3<y1<y2 | D. | y2<y1<y3 |
11. 如图,菱形OBCD在平面直角坐标系中的位置如图所示,顶点B(0,2$\sqrt{3}$),∠DOB=60°,点P是对角线OC上的一个动点,已知A(-1,0),则AP+BP的最小值为( )
如图,菱形OBCD在平面直角坐标系中的位置如图所示,顶点B(0,2$\sqrt{3}$),∠DOB=60°,点P是对角线OC上的一个动点,已知A(-1,0),则AP+BP的最小值为( )
 如图,菱形OBCD在平面直角坐标系中的位置如图所示,顶点B(0,2$\sqrt{3}$),∠DOB=60°,点P是对角线OC上的一个动点,已知A(-1,0),则AP+BP的最小值为( )
如图,菱形OBCD在平面直角坐标系中的位置如图所示,顶点B(0,2$\sqrt{3}$),∠DOB=60°,点P是对角线OC上的一个动点,已知A(-1,0),则AP+BP的最小值为( )| A. | 4 | B. | 5 | C. | 3$\sqrt{3}$ | D. | $\sqrt{19}$ |
 2015年12月16-18日,第二届互联网大会在浙江乌镇胜利举行,这说明我国互联网发展走到了世界的前列,尤其是电子商务.据市场调查,天猫超市在销售一种进价为每件40元的护眼台灯中发现:每月销售量y(件)与销售单价x(元)之间的函数关系如图所示.
2015年12月16-18日,第二届互联网大会在浙江乌镇胜利举行,这说明我国互联网发展走到了世界的前列,尤其是电子商务.据市场调查,天猫超市在销售一种进价为每件40元的护眼台灯中发现:每月销售量y(件)与销售单价x(元)之间的函数关系如图所示.