题目内容
13．△ABC中，∠B=∠A+20°，∠C=∠B+10°，求△ABC各内角的度数．分析 将第一个等式代入第二等式，用∠A表示出∠C，再根据三角形的内角和等于180°，列方程求出∠A，然后求解即可．
解答 解：∵∠B=∠A+20°，∠C=∠B+10°，
∴∠C=∠A+20°+10°=∠A+30°，
由三角形内角和定理得，∠A+∠B+∠C=180°，
所以，∠A+∠A+20°+∠A+30°=180°，
解得∠A=$\frac{130°}{3}$，
所以，∠B=$\frac{130°}{3}$+20°=$\frac{190°}{3}$，∠C=$\frac{130°}{3}$+30°=$\frac{220°}{3}$．
点评 本题考查了三角形的内角和定理，用∠A表示出∠C，然后列出关于∠A的方程是解题的关键．
练习册系列答案
相关题目
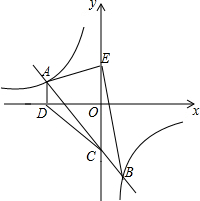如图，一次函数y=ax+b（a≠0）的图象与反比例函数y=$\frac{k}{x}$（k≠0）的图象交于第二象限的点A（m，1），且与y轴交于点C．过点A作x轴的垂线，垂足为点D，连接CD，已知△ADC的面积为$\frac{3}{2}$，且tan∠ACO=1．