Question

8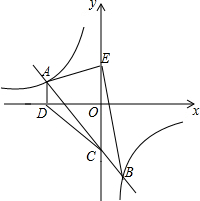．如图，一次函数y=ax+b（a≠0）的图象与反比例函数y=$\frac{k}{x}$（k≠0）的图象交于第二象限的点A（m，1），且与y轴交于点C．过点A作x轴的垂线，垂足为点D，连接CD，已知△ADC的面积为$\frac{3}{2}$，且tan∠ACO=1．
（1）求这个一次函数和反比例函数的解析式；
（2）若点E是点C关于x轴的对称点，点B的纵坐标为-3，求△ABE的面积．

Answer 1

分析 （1）根据三角形的面积公式列方程$\frac{1}{2}$×（-m）×1=$\frac{3}{2}$，得到A（-3，1），把A代入y=$\frac{k}{x}$得到k=-3，求得C（0，-2）由待定系数法即可得到结论；
（2）由点E是点C关于x轴的对称点，得到E（0，2），根据三角形的面积公式即可得到结论．

解答 解：（1）∵A（m，1），△ADC的面积为$\frac{3}{2}$，
∴$\frac{1}{2}$×（-m）×1=$\frac{3}{2}$，
∴m=-3，
∴A（-3，1），
把A代入y=$\frac{k}{x}$得1=$\frac{k}{-3}$，
∴k=-3，
∴反比例函数的解析式为：y=-$\frac{3}{x}$
∵tan∠ACO=1，
∴$\frac{3}{1+OC}=1$，
∴OC=2，
∴C（0，-2）
∴y=ax-2，代入A（-3，1）得1=-3a-2，
∴a=-1，
∴一次函数的解析式为：y=-x-2；

（2）∵点E是点C关于x轴的对称点，
∴E（0，2），
∵点B的纵坐标为-3，
∴-3=-x-2，
∴x=1，
∴△ABE的面积=△ACE的面积+△CBE的面积=$\frac{1}{2}$×4×3+$\frac{1}{2}$×4×1=8．

点评 本题考查的是反比例函数图象与一次函数图象的交点问题，轴对称的性质，解直角三角形，灵活运用数形结合思想求出有关点的坐标和图象的解析式是解题的关键．