题目内容
10．下列各多项式中：①x2-y2，②x3+2，③x2+4x，④x2-10x+25，其中能直接运用公式法分解因式的个数是（ ）| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
分析 分别利用平方差公式以及完全平方公式分解因式得出答案．
解答 解：①x2-y2=（x+y）（x-y），能用公式分解因式；
②x3+2，无法分解因式，
③x2+4x=x（x+4），不能运用公式法分解因式，
④x2-10x+25=（x-5）2，能用公式分解因式；
故选：B．
点评 此题主要考查了公式法分解因式，正确应用公式是解题关键．
练习册系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
20．
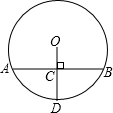如图，已知⊙O的半径OD与弦AB互相垂直，垂足为点C，若AB=16cm，CD=6cm，则⊙O的半径为（ ）
如图，已知⊙O的半径OD与弦AB互相垂直，垂足为点C，若AB=16cm，CD=6cm，则⊙O的半径为（ ）| A． | $\frac{25}{3}$ cm | B． | 10cm | C． | 8cm | D． | $\frac{19}{3}$ cm |
如图，在Rt△ABC中，∠ACB=90，AC=3，BC=4，分别以AB、AC、BC为边在AB同侧作正方形ABEF，ACPQ，BDMC，记四块阴影部分的面积分别为S1、S2、S3、S4，则S1+S2+S3+S4=18．
18．
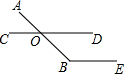如图，点O是∠ABE的边BA上的一点，过点O的直线CD∥BE，若∠AOC=40°，则∠B的度数为（ ）
如图，点O是∠ABE的边BA上的一点，过点O的直线CD∥BE，若∠AOC=40°，则∠B的度数为（ ）| A． | 160° | B． | 140° | C． | 60° | D． | 50° |
5．如果$\sqrt{3+a}$+（5-b）2=0，那么点A（a，b）关于原点对称的点A′的坐标为（ ）
| A． | （3，5） | B． | （3，-5） | C． | （-3，5） | D． | （5，-3） |
15．下列方程中解为x=3的方程是（ ）
| A． | 3x+1=5x-5 | B． | 2（x+3）=-x+9 | C． | 3（1-2x）-2（x+3）=0 | D． | $\frac{x+1}{2}$$-\frac{x-1}{3}$=1 |
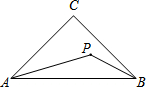如图，在△ABC中，∠C=90°，AC=BC=1，P为△ABC内一个动点，∠PAB=∠PBC，则CP的最小值为$\sqrt{2}$-1．
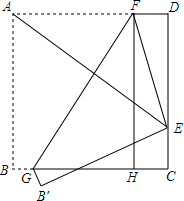如图，将边长为4的正方形ABCD折叠，使得点A落在CD边上的点E处，点B落在点B′处，折痕为GF，FH⊥BC于点H，FG=5
20．下列运算中结果正确的是（ ）
| A． | 3a+2b=5ab | B． | a•a4=a4 | C． | （a3b）2=a6b2 | D． | a6•a2=a12 |