题目内容
20．
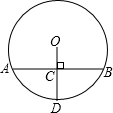如图，已知⊙O的半径OD与弦AB互相垂直，垂足为点C，若AB=16cm，CD=6cm，则⊙O的半径为（ ）| A． | $\frac{25}{3}$ cm | B． | 10cm | C． | 8cm | D． | $\frac{19}{3}$ cm |
分析 连接OA，根据垂径定理求出AC，设⊙O的半径为rcm，根据勾股定理得出方程，求出方程的解即可．
解答 解：连结OA，如图，设⊙O的半径为rcm，
∵OD⊥AB，OD过O，
∴AC=BC=$\frac{1}{2}$AB=8cm，
在Rt△OAC中，∵OA=rcm，OC=OD-CD=（r-6）cm，AC=8cm，
∴（r-6）2+82=r2，
解得r=$\frac{25}{3}$，
即⊙O的半径为$\frac{25}{3}$cm．
故选A．
点评 本题考查了垂径定理和勾股定理，能得出关于r的方程是解此题的关键，注意：垂直于弦的直径平分这条弦．
练习册系列答案
相关题目
17．下列运算正确的是（ ）
| A． | （a-3）2=a2-9 | B． | a2•a4=a8 | C． | $\sqrt{9}$=±3 | D． | x6÷x3=x3 |
如图，点B、E、C、F在一条直线上，∠B=∠DEF，AB=DE，BE=CF，∠F=68°，求∠ACB的度数．
8．
如图，在平面直角坐标系中，有若干个横纵坐标分别为整数的点，其顺序按图中“→”方向排序，如（1，0）→（2，0）→（2，1）→（1，1）→（1，2）→（2，2）…根据这个规律，则第2018个点的横坐标为（ ）
如图，在平面直角坐标系中，有若干个横纵坐标分别为整数的点，其顺序按图中“→”方向排序，如（1，0）→（2，0）→（2，1）→（1，1）→（1，2）→（2，2）…根据这个规律，则第2018个点的横坐标为（ ）| A． | 44 | B． | 45 | C． | 46 | D． | 47 |
15．下列各式中不能用平方差公式计算的是（ ）
| A． | （2x+y）（2x-y） | B． | （x-y）（y-x） | C． | （-x+y）（-x-y） | D． | （x+y）（-x+y） |
5．下列方程组是二元一次方程组的是（ ）
| A． | $\left\{\begin{array}{l}{x-y=1}\\{xy=2}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{\frac{1}{x}-1=y}\\{3x+y=0}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{{x}^{2}-x-2=0}\\{y=x+1}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{4x-y=-1}\\{y=2x+3}\end{array}\right.$ |
