题目内容
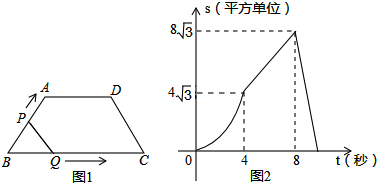
19.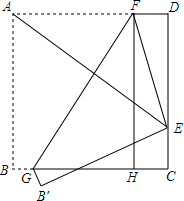 如图,将边长为4的正方形ABCD折叠,使得点A落在CD边上的点E处,点B落在点B′处,折痕为GF,FH⊥BC于点H,FG=5
如图,将边长为4的正方形ABCD折叠,使得点A落在CD边上的点E处,点B落在点B′处,折痕为GF,FH⊥BC于点H,FG=5(1)求证;△GHF≌△EDA;
(2)求线段AF的长.
分析 (1)由折叠的性质得:FG⊥AE,证得∠GFH=90°-∠AFG=∠DAE,再证得四边形DCHF是矩形,得到FH=DC=AD,即可证得△GHF≌△EDA;
(2)由于△GHF≌△EDA,根据全等三角形的性质得到AE=FG=5,由勾股定理求得DE,由折叠的性质知:EF=AF=AD-FD,由勾股定理求得 FD,即可求得结论.
解答 (1)证明:由折叠的性质得:FG⊥AE,
∴∠GFH=90°-∠AFG=∠DAE,
∵正方形ABCD,
∴∠ADE=∠C=90°,AD=DC,
∵FH⊥BC,∴∠DFH=∠FHC=90°,
∴四边形DCHF是矩形,
∴FH=DC=AD,
在△GHF和△EDA中$\left\{\begin{array}{l}{∠GFH=∠DAE}\\{FH=AD}\\{∠FHG=ADE}\end{array}\right.$,
∴△GHF≌△EDA;
(2)解:∵△GHF≌△EDA,
∴AE=FG=5,
∴DE2=AE2-AD2=52-42=32,
由折叠的性质知:EF=AF=AD-FD=4-FD,
由勾股定理得:EF2=FD2+DE2,
即(4-FD)2=FD2+32,
解得:FD=$\frac{7}{8}$,
∴AF=AD-FD=4-$\frac{7}{8}$=$\frac{25}{8}$.
点评 本题主要考查的是翻折的性质、矩形的性质和判定、正方形的性质、勾股定理的应用,证得△GHF≌△EDA是解题的关键.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
7. 如图,在△ABC中,AB=AC,∠A=30°,AC的垂直平分线分别交AB,AC于D,E.连接CD,若CD=1cm,则BD的长为( )
如图,在△ABC中,AB=AC,∠A=30°,AC的垂直平分线分别交AB,AC于D,E.连接CD,若CD=1cm,则BD的长为( )
 如图,在△ABC中,AB=AC,∠A=30°,AC的垂直平分线分别交AB,AC于D,E.连接CD,若CD=1cm,则BD的长为( )
如图,在△ABC中,AB=AC,∠A=30°,AC的垂直平分线分别交AB,AC于D,E.连接CD,若CD=1cm,则BD的长为( )| A. | 1cm | B. | ($\sqrt{3}$-1)cm | C. | $\frac{\sqrt{3}}{2}$cm | D. | $\sqrt{3}$cm |
14.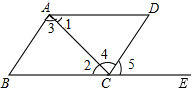 如图,四边形ABCD中,点E在BC延长线上,则下列条件中不能判断AB∥CD的是( )
如图,四边形ABCD中,点E在BC延长线上,则下列条件中不能判断AB∥CD的是( )
 如图,四边形ABCD中,点E在BC延长线上,则下列条件中不能判断AB∥CD的是( )
如图,四边形ABCD中,点E在BC延长线上,则下列条件中不能判断AB∥CD的是( )| A. | ∠3=∠4 | B. | ∠1=∠2 | C. | ∠5=∠ABC | D. | ∠1+∠3+∠D=180° |
4.下列二次根式中,与3$\sqrt{2}$是同类二次根式的是( )
| A. | $\sqrt{2}$ | B. | $\sqrt{24}$ | C. | $\sqrt{27}$ | D. | $\sqrt{50}$ |
11.某校八年级有800名学生,从中随机抽取了100名学生进行立定跳远测试,其中说法错误的是( )
| A. | 这种调查方式是抽样调查 | |
| B. | 每名学生的立定跳远成绩是个体 | |
| C. | 100名学生是样本容量 | |
| D. | 这100名学生的立定跳远成绩是总体的一个样本 |
8.在下面几何体中,其俯视图是三角形的是( )
| A. |  | B. |  | C. |  | D. |  |
9. 如图,AB∥CD,∠DCE=75°,则∠BEF=( )
如图,AB∥CD,∠DCE=75°,则∠BEF=( )
 如图,AB∥CD,∠DCE=75°,则∠BEF=( )
如图,AB∥CD,∠DCE=75°,则∠BEF=( )| A. | 105° | B. | 95° | C. | 80° | D. | 75° |