题目内容
16．
如图，O为码头，A、B两个灯塔与码头O的距离相等，OA，OB为海岸线，一轮船P离开码头，计划沿∠AOB的平分线航行．（1）用尺规作出轮船的预定航线OC；
（2）在航行途中，轮船P始终保持与灯塔A、B的距离相等，试问轮船航行时是否偏离了预定航线？请说明理由．
分析 （1）直接利用角平分线的作法得出符合题意的图形；
（2）利用全等三角形的判定与性质得出答案．
解答 
解：（1）如图所示：OC即为所求．
（2）没有偏离预定航行，
理由如下：
在△AOP与△BOP中，
$\left\{\begin{array}{l}{OA=OB}\\{OP=OP}\\{AP=BP}\end{array}\right.$，
∴△AOP≌△BOP（SSS）．
∴∠AOC=∠BOC，
即点C在∠AOB的平分线上．
点评 此题主要考查了应用设计与作图以及全等三角形的判定与性质，正确应用角平分线的性质是解题关键．
练习册系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
4．下列调查中，适宜采用全面调查的是（ ）
| A． | 了解一批炮弹的杀伤半径 | |
| B． | 了解一批灯泡的使用寿命 | |
| C． | 了解全国人民对政府惩治腐败的满意程度 | |
| D． | 了解本班同学对星期天外出旅游的态度 |
1．
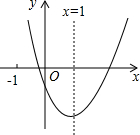二次函数y=ax2+bx+c（a≠0）的图象如图所示，对称轴为x=1，给出下列结论：①abc＞0；②b2=4ac；③4a+2b+c＞0；④3a+c＞0，其中正确的结论是①④．（写出正确命题的序号）
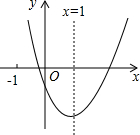二次函数y=ax2+bx+c（a≠0）的图象如图所示，对称轴为x=1，给出下列结论：①abc＞0；②b2=4ac；③4a+2b+c＞0；④3a+c＞0，其中正确的结论是①④．（写出正确命题的序号） 
如图，折叠矩形，使AD边与对角线BD重合，折痕是DG，点A的对应点是E，若AB=2，BC=1，求AG．