题目内容
2．
如图，AC，BD相交于点O，AB∥CD，AD∥BC，E，F分别是OB，OD的中点，求证：四边形AFCE是平行四边形．
分析 由条件AB∥CD，AD∥BC可证到四边形ABCD是平行四边形，根据平行四边形的性质可得OA=OC，OB=OD，要证四边形AFCE是平行四边形，只需证OE=OF即可．
解答 证明：∵AB∥CD，AD∥BC，
∴四边形ABCD是平行四边形，
∴OA=OC，OB=OD．
∵E，F分别是OB，OD的中点，
∴OE=$\frac{1}{2}$OB，OF=$\frac{1}{2}$OD，
∴OE=OF，
∴四边形AFCE是平行四边形．
点评 本题主要考查了平行四边形的判定与性质、线段中点的定义等知识，平行四边形的判定比较多，需结合条件选择合适的判定方法，本题条件与对角线有关，故选择对角线互相平分的四边形是平行四边形这种判定方法．
练习册系列答案
课时训练江苏人民出版社系列答案
相关题目
10．某灯泡厂生产节能灯泡1000只，其中有5只是次品，如果从中任取1只，这只灯泡是次品的概率是（ ）
| A． | $\frac{1}{1000}$ | B． | $\frac{1}{500}$ | C． | $\frac{1}{200}$ | D． | $\frac{95}{1000}$ |
17．八（6）班组织了一次经典朗读比赛，甲、乙两队各9人的比赛成绩如表（10分制）：
（1）甲队成绩的中位数是10分，乙队成绩的众数是9分；
（2）计算乙队的平均成绩和方差；
（3）若选择其中一队参加校级经典朗读比赛则应选乙队．
| 甲 | 7 | 8 | 9 | 7 | 10 | 10 | 10 | 10 | 10 |
| 乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 |
（2）计算乙队的平均成绩和方差；
（3）若选择其中一队参加校级经典朗读比赛则应选乙队．
11．
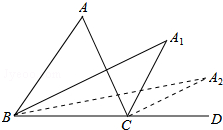如图，在△ABC中，∠A=80，∠ABC的平分线与∠ACD的平分线交于点A1，得∠A1，∠A1BC的平分线与∠A1CD的平分线交于点A2，得∠A2，…，∠A2015BC的平分线与∠A2015CD的平分线交于点A2016，得∠A2016CD，则∠A2016=（ ）
如图，在△ABC中，∠A=80，∠ABC的平分线与∠ACD的平分线交于点A1，得∠A1，∠A1BC的平分线与∠A1CD的平分线交于点A2，得∠A2，…，∠A2015BC的平分线与∠A2015CD的平分线交于点A2016，得∠A2016CD，则∠A2016=（ ）| A． | 80•2-2014 | B． | 80•2-2015 | C． | 80•2-2016 | D． | 80•2-2017 |
