题目内容
 有一个附有进水管的容器,每单位时间内进水量都是一定的,设从某时刻开始的4分钟内只进水、不出水,在随后的8分钟内既进水,又出水,得到时间x(分)与容器内水量y(升)之间的关系如图所示:
有一个附有进水管的容器,每单位时间内进水量都是一定的,设从某时刻开始的4分钟内只进水、不出水,在随后的8分钟内既进水,又出水,得到时间x(分)与容器内水量y(升)之间的关系如图所示:(1)点A表示的意义是什么?
(2)求进水管每分钟进水多少升?出水管每分钟的出水多少升?
(3)如果12分钟以后只放水,不进水,请在图中画出放完容器内水的函数图象;
(4)当4≤x≤12时,请直接写出y与x的函数解析式.
考点:一次函数的应用
专题:
分析:(1)根据坐标系中横纵坐标的意义即可求解;
(2)根据(1)即可求得每分钟的进水量,然后根据从4分钟到12分钟的进水量,即可求得出水的速度;
(3)根据(2)的结果求得放尽水所用的时间即可求出函数解析式,作出图象;
(4)利用待定系数法即可求解.
(2)根据(1)即可求得每分钟的进水量,然后根据从4分钟到12分钟的进水量,即可求得出水的速度;
(3)根据(2)的结果求得放尽水所用的时间即可求出函数解析式,作出图象;
(4)利用待定系数法即可求解.
解答: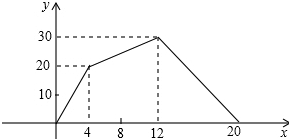 解:(1)4分钟时,进水20升;
解:(1)4分钟时,进水20升;
(2)根据图象知道:
每分钟进水20÷4=5升、
每分钟出水[(12-4)×5-(30-20)]÷(12-4)=
升;
(3)∵12分钟以后只出水不进水,
∴30÷15 4=8分钟,
∴8分钟将水放完,
∴函数解析式为y=30-
(x-12)=-
x+75,
令y=0,解得x=20,
则函数图象如图;
(4)当4≤x≤12时,设解析式为y=kx+b,
依题意得 4k+b=20 12k+b=30,
解得:k=
,b=15,
∴y=
x+15.
 解:(1)4分钟时,进水20升;
解:(1)4分钟时,进水20升;(2)根据图象知道:
每分钟进水20÷4=5升、
每分钟出水[(12-4)×5-(30-20)]÷(12-4)=
| 15 |
| 4 |
(3)∵12分钟以后只出水不进水,
∴30÷15 4=8分钟,
∴8分钟将水放完,
∴函数解析式为y=30-
| 15 |
| 4 |
| 15 |
| 4 |
令y=0,解得x=20,
则函数图象如图;
(4)当4≤x≤12时,设解析式为y=kx+b,
依题意得 4k+b=20 12k+b=30,
解得:k=
| 5 |
| 4 |
∴y=
| 5 |
| 4 |
点评:本题考查了一次函数的应用,解答一次函数的应用问题中,要注意自变量的取值范围还必须使实际问题有意义.

练习册系列答案
相关题目
 如图,已知B,C,D三点在一条直线上,AC⊥BD,DE⊥BD,AB⊥BE,
如图,已知B,C,D三点在一条直线上,AC⊥BD,DE⊥BD,AB⊥BE, 已知BN平分∠ABC,CM平分∠ACB,AM⊥CM,AN⊥BN;
已知BN平分∠ABC,CM平分∠ACB,AM⊥CM,AN⊥BN; 甲、乙两车分别从相距360千米的A、B两地同时相向出发,甲车到B地休息1小时后返回A地时速度提高为原来的
甲、乙两车分别从相距360千米的A、B两地同时相向出发,甲车到B地休息1小时后返回A地时速度提高为原来的 已知:如图,在△ABC中,∠BAC=90°,AB=AC,分别过B、C作过点A的直线l的垂线BD、CE,垂足分别为D、E,求证:DE=BD+CE.
已知:如图,在△ABC中,∠BAC=90°,AB=AC,分别过B、C作过点A的直线l的垂线BD、CE,垂足分别为D、E,求证:DE=BD+CE. 如图是交警在一个路口统计的某个时段来往车辆的车速情况(单位:千米/时)
如图是交警在一个路口统计的某个时段来往车辆的车速情况(单位:千米/时)