题目内容
12.解方程:(1)$\frac{5x-4}{2x-4}$=$\frac{2x+5}{3x-6}$-$\frac{1}{2}$;
(2)$\frac{1}{x+1}$+$\frac{2}{x-1}$=$\frac{4}{{x}^{2}-1}$;
(3)$\frac{8}{4{x}^{2}-1}$+$\frac{2x+3}{1-2x}$=-1;
(4)$\frac{6}{(x+1)(x-2)}$-$\frac{2}{x-2}$=$\frac{-1}{1+x}$.
分析 各方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)去分母得:15x-12=4x+10-3x+6,
移项合并得:14x=28,
解得:x=2,
经检验x=2是增根,分式方程无解;
(2)去分母得:x-1+2x+2=4,
解得:x=1,
经检验x=1是增根,分式方程无解;
(3)去分母得:8-(2x+3)(2x+1)=-4x2+1,
去括号得:8-4x2-8x-3=-4x2+1,
解得:x=$\frac{1}{2}$,
经检验x=$\frac{1}{2}$是增根,分式方程无解;
(4)去分母得:6-2(x+1)=-(x-2),
去括号得:6-2x-2=-x+2,
解得:x=2,
经检验x=2是增根,分式方程无解.
点评 此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
相关题目
2.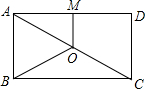 如图,O是矩形ABCD的对称中心,M是AD的中点.若BC=8,OB=5,则OM的长为( )
如图,O是矩形ABCD的对称中心,M是AD的中点.若BC=8,OB=5,则OM的长为( )
 如图,O是矩形ABCD的对称中心,M是AD的中点.若BC=8,OB=5,则OM的长为( )
如图,O是矩形ABCD的对称中心,M是AD的中点.若BC=8,OB=5,则OM的长为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
4.李老师将6份奖品分别放入6个相同礼盒(不透明)中准备将给小英等6位获得“爱集体标兵”称号的同学.这些奖品中有3份是学习机,2份是科普读物,1份是乒乓球拍,小英同学从中随机抽取1份奖品,恰好抽到科普读物的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
2.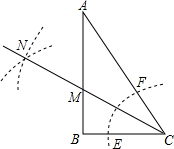 Rt△ABC中,∠B=90°∠A=30°.以C为圆心,小于BC长为半径画弧与AC、BC边交于点F、E.分别以E、F为圆心,大于$\frac{1}{2}$EF为半径画弧,两弧交于点N,若BC=$\sqrt{3}$,则点M到AC的距离是( )
Rt△ABC中,∠B=90°∠A=30°.以C为圆心,小于BC长为半径画弧与AC、BC边交于点F、E.分别以E、F为圆心,大于$\frac{1}{2}$EF为半径画弧,两弧交于点N,若BC=$\sqrt{3}$,则点M到AC的距离是( )
 Rt△ABC中,∠B=90°∠A=30°.以C为圆心,小于BC长为半径画弧与AC、BC边交于点F、E.分别以E、F为圆心,大于$\frac{1}{2}$EF为半径画弧,两弧交于点N,若BC=$\sqrt{3}$,则点M到AC的距离是( )
Rt△ABC中,∠B=90°∠A=30°.以C为圆心,小于BC长为半径画弧与AC、BC边交于点F、E.分别以E、F为圆心,大于$\frac{1}{2}$EF为半径画弧,两弧交于点N,若BC=$\sqrt{3}$,则点M到AC的距离是( )| A. | 1 | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | 3 |
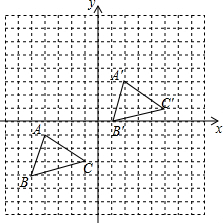 如图所示,将△ABC先向右平移6个单位长度,再向上平移4个单位长度,得到△A′B′C′,△ABC三个顶点的坐标分别为A(-4,-1)、B(-5,-4)、C(-1,-3).
如图所示,将△ABC先向右平移6个单位长度,再向上平移4个单位长度,得到△A′B′C′,△ABC三个顶点的坐标分别为A(-4,-1)、B(-5,-4)、C(-1,-3).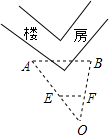 如图,为了测量有障碍物相隔的A、B两点间的距离,请你通过构造位似图形,设计一种测量方案,需要测量的数据用a,b,c,…表示,并求出A、B间的距离.
如图,为了测量有障碍物相隔的A、B两点间的距离,请你通过构造位似图形,设计一种测量方案,需要测量的数据用a,b,c,…表示,并求出A、B间的距离.