题目内容
6．若分式方程$\frac{x+1}{x-4}$=2+$\frac{a}{x-4}$有增根，则a的值为（ ）| A． | 5 | B． | 4 | C． | 3 | D． | 0 |
分析 分式方程去分母转化为整式方程，由分式方程有增根，求出x的值，代入整式方程计算即可求出a的值．
解答 解：去分母得：x+1=2x-8+a，
由分式方程有增根，得到x-4=0，即x=4，
把x=4代入整式方程得：a=5，
故选A
点评 此题考查了分式方程的增根，增根确定后可按如下步骤进行：①化分式方程为整式方程；②把增根代入整式方程即可求得相关字母的值．
练习册系列答案
相关题目
16．下列运算正确的是（ ）
| A． | （2$\sqrt{2}$）2=4 | B． | $\sqrt{\frac{5}{2}}$=$\frac{\sqrt{5}}{2}$ | C． | $\sqrt{{x}^{2}}$=x | D． | $\sqrt{-{x}^{3}}$=-x$\sqrt{-x}$ |
14．在函数y=$\frac{\sqrt{x-3}}{2}$中，自变量x的取值范围是（ ）
| A． | x＞3 | B． | x≥3 | C． | x≠3 | D． | x≤3 |
1．下列计算中正确的是（ ）
| A． | （2a3）2=4a6 | B． | （-a）8÷（-a）3=a5 | C． | a3•a2=a6 | D． | （y3）2=y5 |
18．下列各式从左到右的变形中正确的是（ ）
| A． | $\frac{x-\frac{1}{2}y}{\frac{1}{2}xy}$=$\frac{2x-y}{xy}$ | B． | $\frac{0.2a+b}{a+2b}=\frac{2a+b}{a+2b}$ | ||
| C． | -$\frac{x+1}{x-y}$=$\frac{x-1}{x-y}$ | D． | $\frac{a+b}{a-b}=\frac{a-b}{a+b}$ |
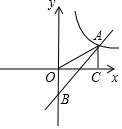如图，点A（5，a）是一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象在第一象限的交点，点B（0，-3）是该一次函数与y轴的交点，连结OA，过点A作AC⊥x轴，垂足为C，若Rt△AOC的面积为5．