题目内容
15.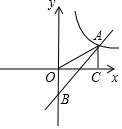 如图,点A(5,a)是一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象在第一象限的交点,点B(0,-3)是该一次函数与y轴的交点,连结OA,过点A作AC⊥x轴,垂足为C,若Rt△AOC的面积为5.
如图,点A(5,a)是一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象在第一象限的交点,点B(0,-3)是该一次函数与y轴的交点,连结OA,过点A作AC⊥x轴,垂足为C,若Rt△AOC的面积为5.(1)求a的值以及反比例函数y=$\frac{m}{x}$的表达式;
(2)求一次函数y=kx+b与x轴的交点坐标.
分析 (1)根据Rt△AOC的面积为5,即可得出m的值,再把点A代入即可得出a的值;
(2)把点A,B的坐标代入一次函数y=kx+b即可得出k,b的值,令y=0即可得出一次函数y=kx+b与x轴的交点坐标.
解答 解:(1)∵Rt△AOC的面积为5,
∴m=10,
∴反比例函数y=$\frac{m}{x}$的表达式为y=$\frac{10}{x}$;
∵点A(5,a)是一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象在第一象限的交点,
∴5a=10,
∴a=2;
(2)把A(5,2),B(0,-3)代入y=kx+b$\left\{\begin{array}{l}{5k+b=2}\\{b=-3}\end{array}\right.$
解得$\left\{\begin{array}{l}{k=1}\\{b=-3}\end{array}\right.$,
∴一次函数的表达式为y=x-3,
令y=0,得x=3,
∴一次函数y=kx+b与x轴的交点坐标(3,0).
点评 本题考查了反比例函数和一次函数的交点问题,涉及的知识有:待定系数法求函数解析式,坐标与图形性质,一次函数与坐标轴的交点,以及反比例函数的图象与性质,熟练掌握待定系数法是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.(-$\frac{1}{3}$)0的计算结果是( )
| A. | -3 | B. | $\frac{1}{3}$ | C. | 1 | D. | -1 |
4. 如图,若a∥b,∠1=60°,则∠2的度数为( )
如图,若a∥b,∠1=60°,则∠2的度数为( )
 如图,若a∥b,∠1=60°,则∠2的度数为( )
如图,若a∥b,∠1=60°,则∠2的度数为( )| A. | 40° | B. | 60° | C. | 120° | D. | 150° |
5.描述一个圆形平移或旋转后正确的说法是( )
| A. | 图形形状与位置都不变 | B. | 图形形状与大小都不变 | ||
| C. | 图形形状与大小都变 | D. | 图形形状与位置都变 |
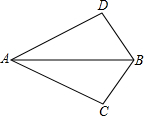 如图,已知AC⊥BC,AD⊥BD.要使△ABC≌△ABD,还需增加一个条件是AD=AC.
如图,已知AC⊥BC,AD⊥BD.要使△ABC≌△ABD,还需增加一个条件是AD=AC.