题目内容
在Rt△ABC中,∠ACB=90°,∠ABC=30°,角平分线BE、CD交于点F,求证:DF=EF.
考点:角平分线的性质,全等三角形的判定与性质
专题:证明题
分析:作出图形,根据三角形的三条角平分线相交于同一点判断出点F在∠A的平分线上,过点F作FG⊥AB于G,作FH⊥AC于H,根据角平分线上的点到角的两边距离相等可得FG=FH,求出∠FDG=∠FEH=75°,然后利用“角角边”证明△DFG和△EFH全等,根据全等三角形对应边相等证明即可.
解答: 证明:如图,∵角平分线BE、CD交于点F,
证明:如图,∵角平分线BE、CD交于点F,
∴点F在∠A的平分线上,
过点F作FG⊥AB于G,作FH⊥AC于H,
则FG=FH,
∵BE、CD都是角平分线,∠ABC=30°,
∴∠FDG=180°-(90°-30°)-
×90°=75°,
∠FEH=(90°-30°)+
×30°=75°,
∴∠FDG=∠FEH=75°,
在△DFG和△EFH中,
,
∴△DFG≌△EFH(AAS),
∴DF=EF.
 证明:如图,∵角平分线BE、CD交于点F,
证明:如图,∵角平分线BE、CD交于点F,∴点F在∠A的平分线上,
过点F作FG⊥AB于G,作FH⊥AC于H,
则FG=FH,
∵BE、CD都是角平分线,∠ABC=30°,
∴∠FDG=180°-(90°-30°)-
| 1 |
| 2 |
∠FEH=(90°-30°)+
| 1 |
| 2 |
∴∠FDG=∠FEH=75°,
在△DFG和△EFH中,
|
∴△DFG≌△EFH(AAS),
∴DF=EF.
点评:本题考查了角平分线上的点到角的两边距离相等的性质,全等三角形的判定与性质,直角三角形两锐角互余的性质,作辅助线构造出全等三角形是解题的关键,难点在于根据度数求出相等的角.

练习册系列答案
相关题目
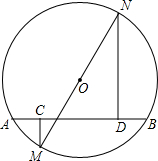 如图,⊙O的直径MN=20cm,弦AB=16cm,MC⊥AB于C,ND⊥AB于D.求ND-CM的值.
如图,⊙O的直径MN=20cm,弦AB=16cm,MC⊥AB于C,ND⊥AB于D.求ND-CM的值.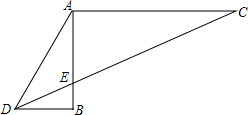 已知,如图AC、BD都垂直于AB,且CD交AB于E,CE=2AD,求证:∠ADE=2∠BDE.
已知,如图AC、BD都垂直于AB,且CD交AB于E,CE=2AD,求证:∠ADE=2∠BDE.