题目内容
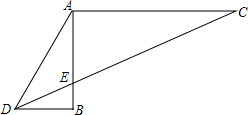 已知,如图AC、BD都垂直于AB,且CD交AB于E,CE=2AD,求证:∠ADE=2∠BDE.
已知,如图AC、BD都垂直于AB,且CD交AB于E,CE=2AD,求证:∠ADE=2∠BDE.考点:直角三角形斜边上的中线,等腰三角形的判定与性质
专题:证明题
分析:取EC的中点F,连接AF,根据直角三角形斜边上的中线等于斜边的一半可得CF=AF=
CE,再求出AD=AF,根据等边对等角可得∠ADE=∠AFD,∠C=∠CAF,再判断出AC∥BD,根据两直线平行,内错角相等可得∠C=∠BDE,然后根据三角形的一个外角等于与它不相邻的两个内角的和证明即可.
| 1 |
| 2 |
解答: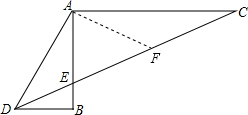 证明:如图,取EC的中点F,连接AF,
证明:如图,取EC的中点F,连接AF,
∵CA⊥AB,
∴CF=AF=
CE,
∴∠C=∠CAF,
又∵CE=2AD,
∴AD=AF,
∴∠ADE=∠AFD,
∵AC、BD都垂直于AB,
∴AC∥BD,
∴∠C=∠BDE,
∵∠AFD=∠C+∠CAF,
∴∠AFD=2∠C,
∴∠ADE=2∠BDE.
 证明:如图,取EC的中点F,连接AF,
证明:如图,取EC的中点F,连接AF,∵CA⊥AB,
∴CF=AF=
| 1 |
| 2 |
∴∠C=∠CAF,
又∵CE=2AD,
∴AD=AF,
∴∠ADE=∠AFD,
∵AC、BD都垂直于AB,
∴AC∥BD,
∴∠C=∠BDE,
∵∠AFD=∠C+∠CAF,
∴∠AFD=2∠C,
∴∠ADE=2∠BDE.
点评:本题考查了直角三角形斜边上的中线等于斜边的一半的性质,平行线的判定与性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记各性质并作出辅助线是解题的关键.

练习册系列答案
相关题目
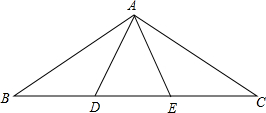 组合作交流的时候对下面一道题产生了争议:如图,在△ABC中,点D、B在BC上,∠B=∠C,∠ADE=∠AED=2∠B,由这些条件,你能得出哪些结论?请证明结论.
组合作交流的时候对下面一道题产生了争议:如图,在△ABC中,点D、B在BC上,∠B=∠C,∠ADE=∠AED=2∠B,由这些条件,你能得出哪些结论?请证明结论.  (1)如图,△ABC是等边三角形,过它的三个顶点分别作对边的平行线,得到一个新的三角形DEF,△DEF是等边三角形吗?你还能找到其他的等边三角形吗?点A,B,C分别是EF,ED,FD的中点吗?请证明你的结论.
(1)如图,△ABC是等边三角形,过它的三个顶点分别作对边的平行线,得到一个新的三角形DEF,△DEF是等边三角形吗?你还能找到其他的等边三角形吗?点A,B,C分别是EF,ED,FD的中点吗?请证明你的结论.