Question

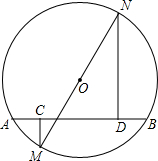如图，⊙O的直径MN=20cm，弦AB=16cm，MC⊥AB于C，ND⊥AB于D．求ND-CM的值．

Answer 1

考点：垂径定理,勾股定理

专题：

分析：连接MD，过O作OE⊥AB于E，交DM于F，求出EF和OF是三角形的中位线，推出ND-MC=2OE，根据垂径定理和勾股定理求出OE长，即可得出答案．

解答：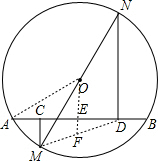
解：连接MD，过O作OE⊥AB于E，交DM于F，
∵MC⊥AB，ND⊥AB，
∴CM∥OF∥ND，
∵OM=ON，
∴MF=FD，CE=DE，
∴OF=

1

2

DN，EF=

1

2

ND，
∴ND-MC=2OE，
连接OA，
由垂径定理得：AE=BE=

1

2

AB=

1

2

×16cm=8cm，OA=

1

2

MN=

1

2

×20=10cm，
∴OE=

102-82

=6（cm），
∴ND-MC=12cm．

点评：本题考查了平行线分线段成比例定理，垂径定理，勾股定理，三角形的中位线的应用，主要考查学生的推理和计算能力．