题目内容
14.为了锻炼学生身体素质,训练定向越野技能,某校在一公园内举行定向越野挑战赛.路线图如图1所示,点E为矩形ABCD边AD的中点,在矩形ABCD的四个顶点处都有定位仪,可监测运动员的越野进程,其中一位运动员P从点B出发,沿着B-E-D的路线匀速行进,到达点D.设运动员P的运动时间为t,到监测点的距离为y.现有y与t的函数关系的图象大致如图2所示,则这一信息的来源是( )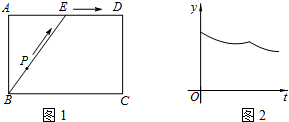
| A. | 监测点A | B. | 监测点B | C. | 监测点C | D. | 监测点D |
分析 根据题意,可以得到各个监测点监测P时,y随t的变化而如何变化,从而可以根据函数图象可以得到选择哪个选项.
解答 解:由题意和图象,可得
由监测点A监测P时,函数值y随t的增大先减小再增大;
由监测点B监测P时,函数值y随t的增大而增大;
由监测点C监测P时,函数值y随t的增大先减小再增大,然后再减小;
由监测点D监测P时,函数值y随t的增大而减小;
故选C.
点评 本题考查动点问题的函数图象,解题的关键是明确各个监测点监测点P时,是如何变化的.

练习册系列答案
相关题目
4.甲、乙、丙、丁四人参加训练,近期的10次百米测试平均成绩都是13.2秒,方差如下表所示
则这四人中发挥最稳定的是( )
| 选手 | 甲 | 乙 | 丙 | 丁 |
| 方差 | 0.030 | 0.019 | 0.121 | 0.022 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
2.有5张形状、大小、质地等均完全相同的卡片,正面分别印有等边三角形、平行四边形、正方形、菱形、圆,背面也完全相同.现将这5张卡片洗匀后正面向下放在桌上,从中随机抽出一张,抽出的卡片正面图案既是中心对称图形,又是轴对称图形的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
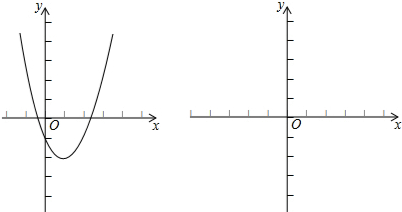
 在边长为1的小正方形网格中,△AOB的顶点均在格点上,
在边长为1的小正方形网格中,△AOB的顶点均在格点上,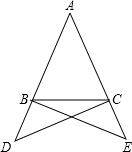 如图,在△ABC中,AB=AC,点D、E分别在AB、AC的延长线上,且∠BCD=$\frac{1}{3}$∠ACB,∠CBE=$\frac{1}{3}$∠ABC.求证:BE=CD.
如图,在△ABC中,AB=AC,点D、E分别在AB、AC的延长线上,且∠BCD=$\frac{1}{3}$∠ACB,∠CBE=$\frac{1}{3}$∠ABC.求证:BE=CD.