题目内容
19. 如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(x>0)的图象交矩形OABC的边AB于点D,交边BC于点E,且BE=2EC.若四边形ODBE的面积为6,则k=3.
如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(x>0)的图象交矩形OABC的边AB于点D,交边BC于点E,且BE=2EC.若四边形ODBE的面积为6,则k=3.
分析 连接OB,由矩形的性质和已知条件得出△OBD的面积=△OBE的面积=$\frac{1}{2}$四边形ODBE的面积=3,在求出△OCE的面积,即可得出k的值.
解答 解:连接OB,如图所示: ∵四边形OABC是矩形,
∵四边形OABC是矩形,
∴∠OAD=∠OCE=∠DBE=90°,△OAB的面积=△OBC的面积,
∵D、E在反比例函数y=$\frac{k}{x}$(x>0)的图象上,
∴△OAD的面积=△OCE的面积,
∴△OBD的面积=△OBE的面积=$\frac{1}{2}$四边形ODBE的面积=3,
∵BE=2EC,∴△OCE的面积=$\frac{1}{2}$△OBE的面积=$\frac{3}{2}$,
∴k=3;
故答案为:3.
点评 本题考查了矩形的性质、三角形面积的计算、反比例函数的图象与解析式的求法;熟练掌握矩形的性质和反比例函数解析式的求法是解决问题的关键.

练习册系列答案
相关题目
9.若△ABC的周长是12cm,则△ABC三条中位线围成的三角形的周长为( )
| A. | 24cm | B. | 6cm | C. | 4cm | D. | 3cm |
14. 如图,在平面直角坐标系中,点A1,A2,A3…都在x轴上,点B1,B2,B3…都在直线y=x上,△OA1B1,△B1A1A2,△B2B1A2,△B2A2A3,△B3B2A3…都是等腰直角三角形,且OA1=1,则点B2015的坐标是( )
如图,在平面直角坐标系中,点A1,A2,A3…都在x轴上,点B1,B2,B3…都在直线y=x上,△OA1B1,△B1A1A2,△B2B1A2,△B2A2A3,△B3B2A3…都是等腰直角三角形,且OA1=1,则点B2015的坐标是( )
 如图,在平面直角坐标系中,点A1,A2,A3…都在x轴上,点B1,B2,B3…都在直线y=x上,△OA1B1,△B1A1A2,△B2B1A2,△B2A2A3,△B3B2A3…都是等腰直角三角形,且OA1=1,则点B2015的坐标是( )
如图,在平面直角坐标系中,点A1,A2,A3…都在x轴上,点B1,B2,B3…都在直线y=x上,△OA1B1,△B1A1A2,△B2B1A2,△B2A2A3,△B3B2A3…都是等腰直角三角形,且OA1=1,则点B2015的坐标是( )| A. | (22014,22014) | B. | (22015,22015) | C. | (22014,22015) | D. | (22015,22014) |
 如图,点P到直线l的距离是1.8cm.(填入具体数值)
如图,点P到直线l的距离是1.8cm.(填入具体数值)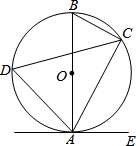 如图,已知AB是⊙O的直径,点C,D在⊙O上,点E在⊙O外,∠EAC=∠B.
如图,已知AB是⊙O的直径,点C,D在⊙O上,点E在⊙O外,∠EAC=∠B.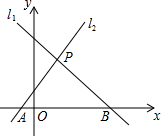 如图,两直线l1:y=-x+4、l2:y=2x+1相交于点P,与x轴分别相交于A、B两点.
如图,两直线l1:y=-x+4、l2:y=2x+1相交于点P,与x轴分别相交于A、B两点.