题目内容
20.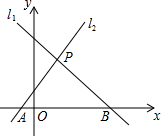 如图,两直线l1:y=-x+4、l2:y=2x+1相交于点P,与x轴分别相交于A、B两点.
如图,两直线l1:y=-x+4、l2:y=2x+1相交于点P,与x轴分别相交于A、B两点.(1)求P点的坐标;
(2)求S△PAB.
分析 (1)根据解方程组,可得P点坐标;
(2)根据自变量与函数的对应关系,可得A、B点坐标,根据三角形的面积公式,可得答案.
解答 解:(1)联立方程组得:$\left\{\begin{array}{l}y=-x+4\\ y=2x+1\end{array}\right.$,
解得$\left\{\begin{array}{l}x=1\\ y=3\end{array}\right.$.
因此P(1,3).
(2)分别求得A$({-\frac{1}{2},0})$,B(4,0),
∴AB=$|{{x_A}-{x_B}}|=\frac{9}{2}$,
∴S△PAB=$\frac{9}{2}$•|yP|•$\frac{1}{2}$=$\frac{1}{2}$×$\frac{9}{2}$×3=$\frac{27}{4}$.
点评 本题考查了两条直线相交或平行问题,解方程组是求交点坐标的关键,又利用了三角形的面积公式.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
10.把多项4x2y-12xy2+4xy分解因式,结果是( )
| A. | 4xy(x-3y) | B. | 4xy(x-3y+1) | C. | 4xy(x+3y-1) | D. | 4xy(x+3y+1) |
 如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(x>0)的图象交矩形OABC的边AB于点D,交边BC于点E,且BE=2EC.若四边形ODBE的面积为6,则k=3.
如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(x>0)的图象交矩形OABC的边AB于点D,交边BC于点E,且BE=2EC.若四边形ODBE的面积为6,则k=3.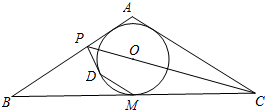 已知等腰△ABC中,AB=AC,∠C的平分线与AB边交于点P,M为△ABC的内切圆⊙O与BC边的切点,作MD∥AC,交⊙O于点D.
已知等腰△ABC中,AB=AC,∠C的平分线与AB边交于点P,M为△ABC的内切圆⊙O与BC边的切点,作MD∥AC,交⊙O于点D. 已知有理数a、b、c在数轴的对应位置如图,则|a-1|+|a-c|+|a-b|可化简为1-c-a+b.
已知有理数a、b、c在数轴的对应位置如图,则|a-1|+|a-c|+|a-b|可化简为1-c-a+b.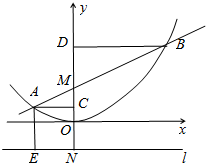 如图所示,过y轴上一点M(0,1)作直线与二次函数y=$\frac{1}{4}$x2的图象交于A、B两点,过A、B两点分别作y轴的垂线,垂足为C、D,直线l过点M关于原点O的对称点N,且与y轴垂直.过点A作l的垂线,垂足为E.
如图所示,过y轴上一点M(0,1)作直线与二次函数y=$\frac{1}{4}$x2的图象交于A、B两点,过A、B两点分别作y轴的垂线,垂足为C、D,直线l过点M关于原点O的对称点N,且与y轴垂直.过点A作l的垂线,垂足为E.