题目内容
4.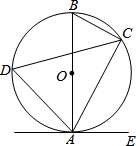 如图,已知AB是⊙O的直径,点C,D在⊙O上,点E在⊙O外,∠EAC=∠B.
如图,已知AB是⊙O的直径,点C,D在⊙O上,点E在⊙O外,∠EAC=∠B.(1)求证:直线AE是⊙O的切线;
(2)若∠D=60°,AB=6时,求劣弧$\widehat{AC}$的长(结果保留π).
分析 (1)根据圆周角定理可得∠ACB=90°,进而可得∠CBA+∠CAB=90°,由∠EAC=∠B可得∠CAE+∠BAC=90°,从而可得直线AE是⊙O的切线;
(2)连接CO,计算出AO长,再利用圆周角定理可得∠AOC的度数,然后利用弧长公式可得答案.
解答 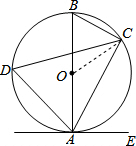 解:(1)∵AB是⊙O的直径,
解:(1)∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠CBA+∠CAB=90°,
∵∠EAC=∠B,
∴∠CAE+∠BAC=90°,
即 BA⊥AE.
∴AE是⊙O的切线.
(2)连接CO,
∵AB=6,
∴AO=3,
∵∠D=60°,
∴∠AOC=120°,
∴$\widehat{AC}$=$\frac{120•π•3}{180}$=2π.
点评 此题主要考查了切线的判定和弧长计算,关键是掌握切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.弧长公式:l=$\frac{nπR}{180}$(弧长为l,圆心角度数为n,圆的半径为R).

练习册系列答案
相关题目
6.在反比例函数y=$\frac{4}{x}$的图象中,阴影部分的面积等于4的有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 如图,已知直线a∥b∥c,直线m,n与a,b,c分别交于点A,C,E,B,D,F,若AC=4,CE=6,BD=3,则DF的值是( )
如图,已知直线a∥b∥c,直线m,n与a,b,c分别交于点A,C,E,B,D,F,若AC=4,CE=6,BD=3,则DF的值是( ) 如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(x>0)的图象交矩形OABC的边AB于点D,交边BC于点E,且BE=2EC.若四边形ODBE的面积为6,则k=3.
如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(x>0)的图象交矩形OABC的边AB于点D,交边BC于点E,且BE=2EC.若四边形ODBE的面积为6,则k=3.
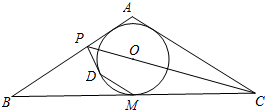 已知等腰△ABC中,AB=AC,∠C的平分线与AB边交于点P,M为△ABC的内切圆⊙O与BC边的切点,作MD∥AC,交⊙O于点D.
已知等腰△ABC中,AB=AC,∠C的平分线与AB边交于点P,M为△ABC的内切圆⊙O与BC边的切点,作MD∥AC,交⊙O于点D.