题目内容
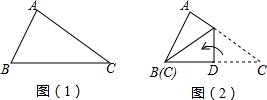
20.已知△ABC和△AEF中,AB=AC,AE=AF,∠BAC=∠EAF,BE、CF交于M,连接MA.(1)如图1,若∠BAC=60°,求∠CMB的度数;
(2)如图2,若∠BAC=90°,则∠CMB=90°;
(3)如图3,若∠BAC=a,则∠AMC=90°+$\frac{1}{2}$α.
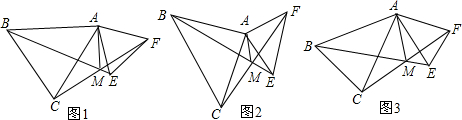
分析 (1)由∠BAC=∠EAF可知∠BAE=∠CAF,依据SAS可知△BAE≌△CAF,由全等三角形的性质可知∠ACM=∠ABM,故此可知点A、B、C、M共圆,由圆周角定理可知∠BMC=∠BAC=60°;
(2)由(1)可知∠BMC=∠BAC;
(3)由(1)的结论可知∠BMC=a,然后由等腰三角形的性质和三角形的内角和定理可得到∠BCA的度数,于是可求得∠BMA的度数,最后可求得∠AMC的度数.
解答 解:(1)∵∠BAC=∠EAF,
∴∠BAC+∠CAE=∠EAF+∠CAE,即∠BAE=∠CAF.
∵在△BAE和△CAF中$\left\{\begin{array}{l}{AB=AC}\\{∠BAE=∠CAF}\\{AE=AF}\end{array}\right.$,
∴△BAE≌△CAF.
∴∠ACM=∠ABM.
∴点A、B、C、M共圆.
∴∠CMB=∠BAC=60°.
(2)由(1)可知:∠CMB=∠BAC.
∵∠BAC=90°,
∴∠CMB=90°.
故答案为:90°.
(3)由(1)可知:∠CMB=∠BAC.
∵∠BAC=α,
∴∠CMB=α.
∵AB=AC,
∴∠ACB=$\frac{1}{2}$×(180°-α)=90°-$\frac{1}{2}$α.
∵由(1)可知点A、B、C、M共圆,
∴∠AMB=∠BCA=90°-$\frac{1}{2}$α.
∴∠AMC=∠AMB+∠BMC=90°-$\frac{1}{2}$α+α=90°+$\frac{1}{2}$α.
故答案为:90°+$\frac{1}{2}$α.
点评 本题主要考查的是全等三角形的性质和判定、圆周角定理、四点共圆,证得点A、B、C、M共圆是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.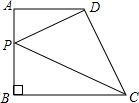 如图,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AD=6,AB=7,BC=8,点P是AB上一个动点.
如图,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AD=6,AB=7,BC=8,点P是AB上一个动点.
(1)当AP=3时,△DAP与△CBP相似吗?请说明理由.
(2)求PD+PC的最小值.
 如图,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AD=6,AB=7,BC=8,点P是AB上一个动点.
如图,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AD=6,AB=7,BC=8,点P是AB上一个动点.(1)当AP=3时,△DAP与△CBP相似吗?请说明理由.
(2)求PD+PC的最小值.
10.已知直线$y=-\frac{3}{5}x+6$,它与坐标轴围成的三角形的面积为( )
| A. | 6 | B. | 10 | C. | 25 | D. | 30 |
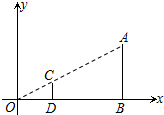 如图,在直角坐标系中,有两点A(6,3)、B(6,0).以原点O为位似中心,相似比为$\frac{1}{3}$,在第一象限内把线段AB缩小后得到线段CD,则点C的坐标为(2,1).
如图,在直角坐标系中,有两点A(6,3)、B(6,0).以原点O为位似中心,相似比为$\frac{1}{3}$,在第一象限内把线段AB缩小后得到线段CD,则点C的坐标为(2,1). 如图,身高1.6m的小王晚上沿箭头方向散步至一路灯下,他想通过测量自己的影长来估计路灯的高度,具体做法如下:先从路灯底部向东走20步到M处,发观自己的影子端点刚好在两盏路灯的中间点P处,继续沿刚才自己的影子走5步到P处,此时影子的端点在Q处.
如图,身高1.6m的小王晚上沿箭头方向散步至一路灯下,他想通过测量自己的影长来估计路灯的高度,具体做法如下:先从路灯底部向东走20步到M处,发观自己的影子端点刚好在两盏路灯的中间点P处,继续沿刚才自己的影子走5步到P处,此时影子的端点在Q处.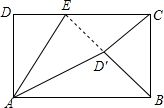 如图,矩形ABCD中,AD=4,AB=7,点E为DC上一动点,△ADE沿AE折叠,点D落在矩形ABCD内一点D′处,若△BCD′为等腰三角形,则DE的长为$\frac{4}{3}$$\sqrt{3}$或$\frac{32-4\sqrt{15}}{7}$.
如图,矩形ABCD中,AD=4,AB=7,点E为DC上一动点,△ADE沿AE折叠,点D落在矩形ABCD内一点D′处,若△BCD′为等腰三角形,则DE的长为$\frac{4}{3}$$\sqrt{3}$或$\frac{32-4\sqrt{15}}{7}$.
 如图,一次函数y=3x+3的图象与x轴交于点A,与y轴交于点B,二次函数y=ax2+bx+c的图象经过点A,B,C,且点C的坐标为(3,0).
如图,一次函数y=3x+3的图象与x轴交于点A,与y轴交于点B,二次函数y=ax2+bx+c的图象经过点A,B,C,且点C的坐标为(3,0).