题目内容
9.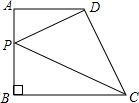 如图,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AD=6,AB=7,BC=8,点P是AB上一个动点.
如图,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AD=6,AB=7,BC=8,点P是AB上一个动点.(1)当AP=3时,△DAP与△CBP相似吗?请说明理由.
(2)求PD+PC的最小值.
分析 (1)由题意可知∠A=∠B=90°,AP=3,PB=4,故此$\frac{AP}{AD}=\frac{BP}{BC}=\frac{1}{2}$,从而可证明△DAP与△CBP相似;
(2)作点D关于AB的对称点D′,连接D′C交BA于点P.过点D′作D′E⊥BC,垂足为E.依据勾股定理求得D′C的长即可.
解答 解:(1)∵∠ABC=90°,AD∥BC,
∴∠BAD=90°.
∴∠A=∠B=90°.
∵AP=3,AB=7,
∴PB=4.
∴$\frac{AP}{AD}=\frac{3}{6}=\frac{1}{2}$,$\frac{PB}{BC}=\frac{4}{8}=\frac{1}{2}$.
∴$\frac{AP}{AD}=\frac{BP}{BC}$.
∴△DAP∽△CBP.
(2)如图所示:点D关于AB的对称点D′,连接D′C交BA于点P,过点D′作D′E⊥BC,垂足为E.
∵点D与点D′关于AB对称,
∴PD=D′P.
∴PD+PC=D′P+PC=D′C.
在Rt△D′EC中,由勾股定理得:D′C=$\sqrt{D′{E}^{2}+E{C}^{2}}$=$\sqrt{{7}^{2}+1{4}^{2}}$=7$\sqrt{5}$.
∴PD+PC的最小值为7$\sqrt{5}$.
点评 本题主要考查的相似三角形的判定、轴对称最短路径问题,掌握本题的辅助线的作法是解题的关键.

练习册系列答案
相关题目
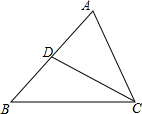 如图,在△ABC中,CD是AB边上的中线,已知∠B=45°,tan∠ACB=2,AC=$\sqrt{5}$,求:
如图,在△ABC中,CD是AB边上的中线,已知∠B=45°,tan∠ACB=2,AC=$\sqrt{5}$,求:
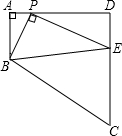 如图,在直角梯形ABCD中,AB∥CD,∠A=90°,AB=2,AD=5,P是AD上一动点(不与A、D重合),PE⊥BP,PE交DC于点E.
如图,在直角梯形ABCD中,AB∥CD,∠A=90°,AB=2,AD=5,P是AD上一动点(不与A、D重合),PE⊥BP,PE交DC于点E.
 已知二次函数的图象经过A(3,0),B(0,-3),C(-2,5)三点.
已知二次函数的图象经过A(3,0),B(0,-3),C(-2,5)三点. 如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数y=$\frac{1}{x}$的图象上.若点B在反比例函数y=$\frac{k}{x}$的图象上,则k的值为-4.
如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数y=$\frac{1}{x}$的图象上.若点B在反比例函数y=$\frac{k}{x}$的图象上,则k的值为-4. 如图,已知∠AOB=60°,点P在边OA上,OP=10,点M,N在边OB上,PM=PN,若MN=2,则OM=4.
如图,已知∠AOB=60°,点P在边OA上,OP=10,点M,N在边OB上,PM=PN,若MN=2,则OM=4.