题目内容
17．
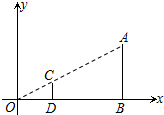如图，在直角坐标系中，有两点A（6，3）、B（6，0）．以原点O为位似中心，相似比为$\frac{1}{3}$，在第一象限内把线段AB缩小后得到线段CD，则点C的坐标为（2，1）．
分析 根据位似变换的性质可知，△ODC∽△OBA，相似比是$\frac{1}{3}$，根据已知数据可以求出点C的坐标．
解答 解：由题意得，△ODC∽△OBA，相似比是$\frac{1}{3}$，
∴$\frac{OD}{OB}$=$\frac{DC}{AB}$，
又∵OB=6，AB=3，
∴OD=2，CD=1，
∴点C的坐标为：（2，1），
故答案为：（2，1）．
点评 本题考查的是位似变换，掌握位似变换与相似的关系是解题的关键，注意位似比与相似比的关系的应用．
练习册系列答案
相关题目
8．对于抛物线y=5（x+2）2+6，下列说法正确的是（ ）
| A． | 开口向下，顶点坐标为（2，6） | B． | 开口向下，顶点坐标为（-2，6） | ||
| C． | 开口向上，顶点坐标为（-2，6） | D． | 开口向上，顶点坐标为（-2，-6） |
5．下列函数关系中表示一次函数的有（ ）
①y=2x-1；②y=$\frac{1}{2x}$；③y=100-3x；④s=pr2．
①y=2x-1；②y=$\frac{1}{2x}$；③y=100-3x；④s=pr2．
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
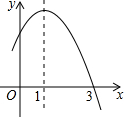已知二次函数y=-x2+2x+m的部分图象如图所示，则关于x的一元二次方程-x2+2x+m=0的解为x1=-1，x2=3，不等式-x2+2x+m＞0的解集为-1＜x＜3．
9．把点A（-2，1）向右平移3个单位长度，再向上平移2个单位长度后得到点B，点B的坐标是（ ）
| A． | （1，3） | B． | （-5，3） | C． | （1，-3） | D． | （-5，-1） |
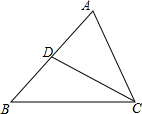如图，在△ABC中，CD是AB边上的中线，已知∠B=45°，tan∠ACB=2，AC=$\sqrt{5}$，求：