题目内容
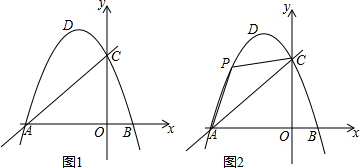
15.等腰Rt△ABC中,∠BCA=90°,BC=AC,点A,C分别在x轴,y轴上.(1)点E在x轴上,且∠CEA=45°,连BE,求证:AE⊥BE;
(2)在(1)的条件下,判断线段BE、AE、CO之间的数量关系,写出你的结论并证明.
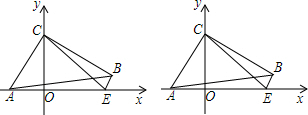
分析 (1)根据等腰直角三角形的性质得到∠ABC=45°,由∠CEA=45°,得到∠ABC=∠AEC,推出A,E,B,C四点共圆,根据圆内接四边形的性质得到∠ACB+∠AEB=180°,即可得到结论;
(2)过C作CH⊥EB,交EB的延长线于H,得到四边形COEH是矩形,推出矩形COEH是正方形,于是得到OC=OE=HE,证得△ACO≌△HCB,根据全等三角形的性质得到AO=HB,由AE=AO+OE,BE=HE-BH,于是得到结论.
解答 (1)证明:∵∠BCA=90°,BC=AC,
∴∠ABC=45°,
∵∠CEA=45°,
∴∠ABC=∠AEC,
∴A,E,B,C四点共圆,
∴∠ACB+∠AEB=180°,
∴∠AEB=90°,
∴AE⊥BE;
(2)解:AE+BE=2OC,
理由:过C作CH⊥EB,交EB的延长线于H,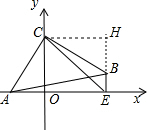
∴∠H=∠EOC=∠OEH=90°,
∴四边形COEH是矩形,
∵∠OEC=45°,
∴OC=OE,
∴矩形COEH是正方形,
∴OC=OE=HE,
∵∠ACB=∠HCO=90°,
∴∠ACO=∠HCB,
在△ACO与△CHB中,$\left\{\begin{array}{l}{∠AOC=∠H}\\{∠ACO=∠HCB}\\{AC=BC}\end{array}\right.$,
∴△ACO≌△HCB,
∴AO=HB,
∵AE=AO+OE,BE=HE-BH,
∴AE+BE=2OC.
点评 本题考查了全等三角形的判定与性质,等腰直角三角形的性质,四点共圆,圆内接四边形的性质,正确的作出辅助线构造全等三角形是解题的关键.

练习册系列答案
相关题目
5.当a=-1时,代数式(a+1)2+a(a+3)的值等于( )
| A. | -4 | B. | 4 | C. | -2 | D. | 2 |
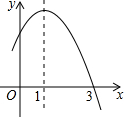 已知二次函数y=-x2+2x+m的部分图象如图所示,则关于x的一元二次方程-x2+2x+m=0的解为x1=-1,x2=3,不等式-x2+2x+m>0的解集为-1<x<3.
已知二次函数y=-x2+2x+m的部分图象如图所示,则关于x的一元二次方程-x2+2x+m=0的解为x1=-1,x2=3,不等式-x2+2x+m>0的解集为-1<x<3.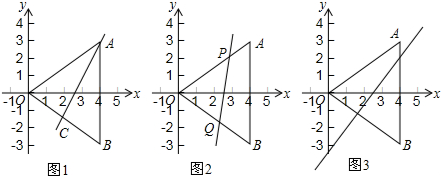
 如图,△ABC两条角平分线BD,CE相交于点O,∠A=60°,求证:CD+BE=BC.
如图,△ABC两条角平分线BD,CE相交于点O,∠A=60°,求证:CD+BE=BC.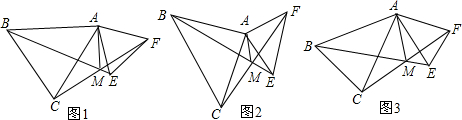
 画图并计算:已知线段EF=30cm,延长EF到B,使FB=EF,延长FE到A,使AE=EB,求AB的长.
画图并计算:已知线段EF=30cm,延长EF到B,使FB=EF,延长FE到A,使AE=EB,求AB的长.