题目内容
3.一艘船在相距120千米的两个码头间航行,去时顺水用了4小时,回来时逆水用了5小时,则水速为( )| A. | 2千米/小时 | B. | 3千米/小时 | C. | 4千米/小时 | D. | 5千米/小时 |
分析 设静水速度为x千米/小时,水流速度为y千米/小时,求得顺水所行路程与逆水所行路程列出方程组解答即可.
解答 解:设静水速度为x千米/小时,水流速度为y千米/小时,由题意得
$\left\{\begin{array}{l}{4(x+y)=120}\\{5(x-y)=120}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=27}\\{y=3}\end{array}\right.$
答:静水速度为27千米/小时,水流速度为3千米/小时.
故选:B.
点评 此题考查二元一次方程组的实际运用,掌握静水速度、水流速度、顺水速度、逆水速度是解决问题的关键.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
14.甲、乙两人比赛投篮球,以命中率(投进球数与投球次数的比值)来比较投球成绩的好坏,表为两人投篮球的记录:
得知他们的成绩一样好,下面有四个a、b的关系式:
①a-b=5;②a+b=18;③a:b=2:1;④a:18=2:3.
其中正确的是( )
| 学生 | 投进球数 | 没投进球数 | 投球次数 |
| 甲 | 10 | 5 | 15 |
| 乙 | a | b | 18 |
①a-b=5;②a+b=18;③a:b=2:1;④a:18=2:3.
其中正确的是( )
| A. | ①②③ | B. | ①③④ | C. | ①②③④ | D. | ②③④ |
18.设有一次函数y=kx+3,当x=-1时,y>1;当x=4时,y>-1,则k的取值范围是( )
| A. | -1<k<2 | B. | -1<k<1 | C. | 1<k<2 | D. | 1<k<3 |
12.下列算结果正确的是( )
| A. | -8-(-3)=5 | B. | (-2.5)-(+7.2)=4.7 | C. | (-$\frac{2}{5}$)-(-$\frac{1}{4}$)=-$\frac{3}{20}$ | D. | 5-(-6)=-1 |
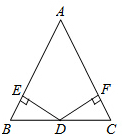 如图,在△ABC中,点D是边BC的中点,DE⊥AB,DF⊥AC,垂足分别为点E、F,且DE=DF.试判断△ABC的形状,并证明你的结论.
如图,在△ABC中,点D是边BC的中点,DE⊥AB,DF⊥AC,垂足分别为点E、F,且DE=DF.试判断△ABC的形状,并证明你的结论.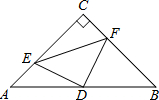 如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E,F分别在AC,BC边上运动(点E不与点A,C重合),且保持ED⊥FD,连接DE,DF,EF,在此运动变化的过程中,有下列结论:
如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E,F分别在AC,BC边上运动(点E不与点A,C重合),且保持ED⊥FD,连接DE,DF,EF,在此运动变化的过程中,有下列结论: