题目内容
17.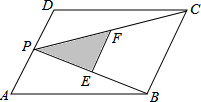 如图,P为平行四边形ABCD边AD上一点,E、F分别为PB、PC的中点,若△PEF的面积S1=1,则?ABCD的面积S=8.
如图,P为平行四边形ABCD边AD上一点,E、F分别为PB、PC的中点,若△PEF的面积S1=1,则?ABCD的面积S=8.
分析 利用三角形中位线定理得出EF∥BC,EF=$\frac{1}{2}$BC,再利用相似三角形的判定与性质得出$\frac{{S}_{△PEF}}{{S}_{△PBC}}$=$\frac{1}{4}$,进而利用平行四边形的面积求法得出答案.
解答 解:∵E,F分别为PB,PC的中点,
∴EF∥BC,EF=$\frac{1}{2}$BC,
∴△PEF∽△PBC,
∴$\frac{EF}{BC}$=$\frac{1}{2}$,
∴$\frac{{S}_{△PEF}}{{S}_{△PBC}}$=$\frac{1}{4}$,
∵S1=1,
∴S△PBC=4,
∵四边形ABCD是平行四边形,
∴S?ABCD=2×4=8.
故答案为:8.
点评 此题主要考查了平行四边形的性质以及相似三角形的判定与性质以及三角形中位线定理等知识,得出$\frac{{S}_{△PEF}}{{S}_{△PBC}}$=$\frac{1}{4}$是解题关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
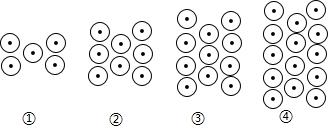
7.下列图形都是由同样大小的基本图形按一定规律所组成的,其中第①个图形中一共有5个基本图形,第②个图形中一共有8个基本图形,第③个图形中一共有11个基本图形,第④个图形中一共有14个基本图形,…,按此规律排列,则第⑧个图形中基本图形的个数为( )

| A. | 23 | B. | 24 | C. | 26 | D. | 29 |
8.如图,水平放置的几何体中,主视图不是长方形的是( )
| A. |  | B. |  | C. |  | D. |  |
12.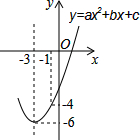 如图,已知顶点为(-3,-6)的抛物线y=ax2+bx+c经过点(-1,-4),则下列结论中错误的是( )
如图,已知顶点为(-3,-6)的抛物线y=ax2+bx+c经过点(-1,-4),则下列结论中错误的是( )
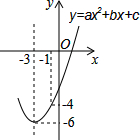 如图,已知顶点为(-3,-6)的抛物线y=ax2+bx+c经过点(-1,-4),则下列结论中错误的是( )
如图,已知顶点为(-3,-6)的抛物线y=ax2+bx+c经过点(-1,-4),则下列结论中错误的是( )| A. | b2>4ac | |
| B. | ax2+bx+c≥-6 | |
| C. | 关于x的一元二次方程ax2+bx+c=-4的两根分别为-5和-1 | |
| D. | 若点(-2,m),(-5,n)在抛物线上,则m>n |
2.下列运算中,结果正确的是( )
| A. | 2a+3b=5ab | B. | a2•a3=a6 | C. | (a4)2=a8 | D. | a6÷a3=a2 |
7.济宁市某经济开发区,今年一月份工业产值达10亿元,第一季度总产值为75亿元,二、三月平均每月增长率是多少,若设平均每月的增长率为x,根据题意,可列方程为( )
| A. | 10(1+x)2=75 | B. | 10+10(1+x)+10(1+x)2=75 | ||
| C. | 10(1+x)+10(1+x)2=75 | D. | 10+10(1+x)2=75 |
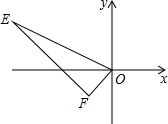 如图,点E(-4,2),F(-1,-1),以点O为位似中心,在点O的另一侧,按比例尺1:2,把△EFO缩小,则点E的对应点E′的坐标为(2,-1).
如图,点E(-4,2),F(-1,-1),以点O为位似中心,在点O的另一侧,按比例尺1:2,把△EFO缩小,则点E的对应点E′的坐标为(2,-1).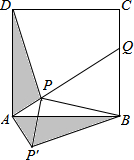 如图,点P是正方形ABCD内一点,点P到点A、B和D的距离分别为1,2$\sqrt{2}$,$\sqrt{10}$,△ADP沿点A旋转至△ABP′,连结PP′,并延长AP与BC相交于点Q.
如图,点P是正方形ABCD内一点,点P到点A、B和D的距离分别为1,2$\sqrt{2}$,$\sqrt{10}$,△ADP沿点A旋转至△ABP′,连结PP′,并延长AP与BC相交于点Q.