题目内容
1.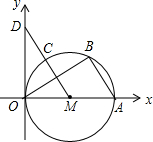 如图,直径为OA的圆M与x轴交于点O,A,点B,C把半圆OA分为三等份,连接MC并延长交y轴于点D.
如图,直径为OA的圆M与x轴交于点O,A,点B,C把半圆OA分为三等份,连接MC并延长交y轴于点D.(1)求∠BAO的度数.
(2)求证:△OMD≌△BAO.
分析 (1)连接BM,由点B,C把半圆OA分为三等份可知:∠BMA=$\frac{1}{3}$×180°=60°,所以△ABM是等边三角形,所以∠BAO=60°.
(2)由(1)可知,∠DMO=∠BAO=60°,且OM=MA=AB,所以△OMD≌△BAO.
解答 解:(1)连接BM,
∵点B,C把半圆OA分为三等份,
∴∠BMA=$\frac{1}{3}$×180°=60°,
又∵MB=MA,
∴△ABM是等边三角形,
∴∠BAO=60°,
(2)∵点B,C把半圆OA分为三等份,
∴∠DMO=$\frac{1}{3}$×180°=60°,
∴∠DMO=∠BAO,
∵AO是⊙M的直径,
∴∠OBA=90°,
由(1)可知:MA=AB,
∴OM=MA=AB,
在△OMD与△BAO中,
$\left\{\begin{array}{l}{∠DMO=∠BAO}\\{OM=AB}\\{∠DOM=∠OBA}\end{array}\right.$,
∴△OMD≌△BAO(ASA).
点评 本题考查圆的综合问题,涉及圆周角定理,弧、弦、圆心角之间的关系,全等三角形的判定,等边三角形的性质,需要学生灵活运用所学知识解决.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
11.在平面直角坐标系中,下列函数的图象经过原点的是( )
| A. | y=-2x+1 | B. | y=-2x | C. | y=-$\frac{2}{x}$ | D. | y=-x2+1 |
12.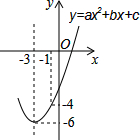 如图,已知顶点为(-3,-6)的抛物线y=ax2+bx+c经过点(-1,-4),则下列结论中错误的是( )
如图,已知顶点为(-3,-6)的抛物线y=ax2+bx+c经过点(-1,-4),则下列结论中错误的是( )
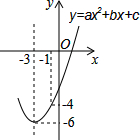 如图,已知顶点为(-3,-6)的抛物线y=ax2+bx+c经过点(-1,-4),则下列结论中错误的是( )
如图,已知顶点为(-3,-6)的抛物线y=ax2+bx+c经过点(-1,-4),则下列结论中错误的是( )| A. | b2>4ac | |
| B. | ax2+bx+c≥-6 | |
| C. | 关于x的一元二次方程ax2+bx+c=-4的两根分别为-5和-1 | |
| D. | 若点(-2,m),(-5,n)在抛物线上,则m>n |
10.对于两个不相等的实数a、b,我们规定符号max{a,b}表示a、b中较大的数,如:max{2,4}=4.按照这个规定.方程max{x,-x}=$\frac{2x+1}{x}$的解为( )
| A. | $1-\sqrt{2}$ | B. | $2-\sqrt{2}$ | C. | $1-\sqrt{2}$或$1+\sqrt{2}$ | D. | $1+\sqrt{2}$或-1 |
11.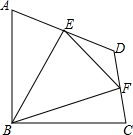 如图,在四边形ABCD中,∠ABC=90°,AB=BC=2$\sqrt{2}$,E、F分别是AD、CD的中点,连接BE、BF、EF.若四边形ABCD的面积为6,则△BEF的面积为( )
如图,在四边形ABCD中,∠ABC=90°,AB=BC=2$\sqrt{2}$,E、F分别是AD、CD的中点,连接BE、BF、EF.若四边形ABCD的面积为6,则△BEF的面积为( )
 如图,在四边形ABCD中,∠ABC=90°,AB=BC=2$\sqrt{2}$,E、F分别是AD、CD的中点,连接BE、BF、EF.若四边形ABCD的面积为6,则△BEF的面积为( )
如图,在四边形ABCD中,∠ABC=90°,AB=BC=2$\sqrt{2}$,E、F分别是AD、CD的中点,连接BE、BF、EF.若四边形ABCD的面积为6,则△BEF的面积为( )| A. | 2 | B. | $\frac{9}{4}$ | C. | $\frac{5}{2}$ | D. | 3 |
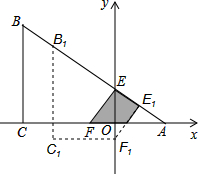 如图,有一张直角三角形纸片ABC,∠ACB=90°,∠B=60°,BC=3,直角边AC在x轴上,B点在第二象限,A($\sqrt{3}$,0),AB交y轴于E,将纸片过E点折叠使BE与EA所在的直线上,得到折痕EF(F在x轴上),再展开还原沿EF剪开得到四边形BCFE,然后把四边形BCFE从E点开始沿射线EA方向平行移动,至B点到达A点停止(记平移后的四边形为B1C1F1E1).在平移过程中,设平移的距离BB1=x,四边形B1C1F1E1与△AEF重叠的面积为S.
如图,有一张直角三角形纸片ABC,∠ACB=90°,∠B=60°,BC=3,直角边AC在x轴上,B点在第二象限,A($\sqrt{3}$,0),AB交y轴于E,将纸片过E点折叠使BE与EA所在的直线上,得到折痕EF(F在x轴上),再展开还原沿EF剪开得到四边形BCFE,然后把四边形BCFE从E点开始沿射线EA方向平行移动,至B点到达A点停止(记平移后的四边形为B1C1F1E1).在平移过程中,设平移的距离BB1=x,四边形B1C1F1E1与△AEF重叠的面积为S.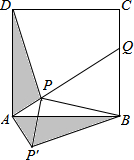 如图,点P是正方形ABCD内一点,点P到点A、B和D的距离分别为1,2$\sqrt{2}$,$\sqrt{10}$,△ADP沿点A旋转至△ABP′,连结PP′,并延长AP与BC相交于点Q.
如图,点P是正方形ABCD内一点,点P到点A、B和D的距离分别为1,2$\sqrt{2}$,$\sqrt{10}$,△ADP沿点A旋转至△ABP′,连结PP′,并延长AP与BC相交于点Q.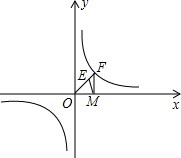 已知:反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点B(1,1)
已知:反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点B(1,1)