题目内容
20.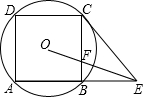 如图,四边形ABCD是⊙O的内接正方形,延长AB至点P,使BP=AB,连接PC.
如图,四边形ABCD是⊙O的内接正方形,延长AB至点P,使BP=AB,连接PC.(1)求证:直线PC与⊙O的相切;
(2)连接PO,若正方形边长为2,求PO的长.
分析 (1)连接OC,由O为正方形的中心得到∠OCB为45°,再由AB=BC=BE,得到三角形BCE为等腰直角三角形,即∠BCE为45°,进而确定出∠OCE为直角,即CE垂直于OC,可得证;
(2)连接OB,过O作OG垂直于AB,利用垂径定理和等腰直角三角形得到OG=AG=BG=$\frac{1}{2}$AB=1,可得出GP=3,然后根据勾股定理即可求出PO的长.
解答 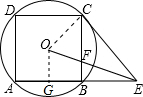 解:(1)连接OC,
解:(1)连接OC,
∵O为正方形ABCD的中心,
∴∠OCB=45°,
∵AB=BC=BP,∠CBP=90°,
∴△CBP为等腰直角三角形,即∠BCP=45°,
∴∠OCP=∠OCB+∠BCP=90°,
∴CP⊥OC,
∴直线PC与⊙O的相切;
(2)连接OB,
∵O为正方形ABCD的中心,
∴∠OBG=45°,
过O作OG⊥AB,可得出OG=AG=BG=$\frac{1}{2}$AB=1,
∵AB=BP=2,
∴PG=3,
∴OP=$\sqrt{G{P}^{2}+O{G}^{2}}$=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$.
点评 此题考查了切线的判定,正方形的性质,垂径定理,以及等腰直角三角形的判定与性质,熟练掌握切线的判定方法是解本题的关键.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
4.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
5.在某校举行的“汉字听写”大赛中,七名学生听写汉字的个数分别为350,310,320,250,310,340,360,则这组数据的中位数是( )
| A. | 330 | B. | 320 | C. | 310 | D. | 250 |
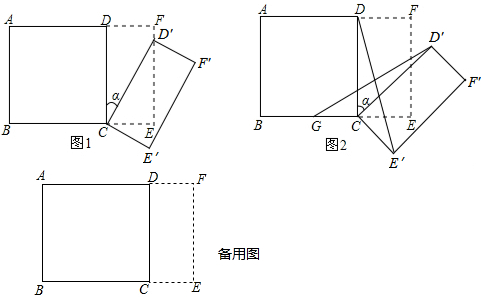
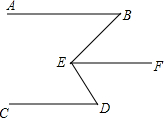 如图,已知∠B=∠BEF,EF∥CD,试判断AB与CD是否平行?
如图,已知∠B=∠BEF,EF∥CD,试判断AB与CD是否平行? 阅读下题及其证明过程.
阅读下题及其证明过程.