题目内容
12. 如图,已知Rt△ABC中,∠C=90°,∠A=30°.按下列步骤作图:分别以A、B为圆心,以大于$\frac{1}{2}$AB的长为半径作弧,两弧相交于点P和Q作直线PQ,分别交AC于点D,交AB于点E;连接BD.则下列结论中:①AD=BD,②∠CBD=30°③BC=$\frac{1}{2}$AB;④S△ABC=4S△BCD正确的个数有( )
如图,已知Rt△ABC中,∠C=90°,∠A=30°.按下列步骤作图:分别以A、B为圆心,以大于$\frac{1}{2}$AB的长为半径作弧,两弧相交于点P和Q作直线PQ,分别交AC于点D,交AB于点E;连接BD.则下列结论中:①AD=BD,②∠CBD=30°③BC=$\frac{1}{2}$AB;④S△ABC=4S△BCD正确的个数有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据作已知线段的垂直平分线可对①进行判断;利用∠DBA=∠CBD=30°可对②进行判断;利用含30度的直角三角形三边的关系可对③进行判断;通过证明△DCB≌△DEB≌△DEA,可对④进行判断.
解答 解:①用作法可得PQ垂直平分AB,则AD=BD,故此选项正确;
②因为DA=DB,则∠A=∠DBA=30°,则∠CBD=30°,故此选项正确;
③∵∠C=90°,∠A=30°,
∴BC=$\frac{1}{2}$AB,故此选项正确;
④由以上可得:
在△DCB和△DEB中,
$\left\{\begin{array}{l}{∠C=∠BED}\\{∠CBD=∠DBE}\\{BD=BD}\end{array}\right.$
∴△DCB≌△DEB(AAS),
在△ADE和△BDE中,
$\left\{\begin{array}{l}{DE=DE}\\{∠AED=∠BED}\\{AE=BE}\end{array}\right.$,
∴△ADE≌△BDE(SAS),
故△DCB≌△DEB≌△DEA,
∴S△ABC=3S△BCD,故此选项错误.
故选:C.
点评 本题考查了作图-基本作图:作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线.

练习册系列答案
相关题目
2. 如图,已知长方形纸片ABCD在平面直角坐标系中,将该纸片沿AC对折,使得点B到达点E的位置,点A的坐标为(0,a),点B的坐标为(2,a),若∠BAC=67.5°,|a|>$\sqrt{2}$,则点E在( )
如图,已知长方形纸片ABCD在平面直角坐标系中,将该纸片沿AC对折,使得点B到达点E的位置,点A的坐标为(0,a),点B的坐标为(2,a),若∠BAC=67.5°,|a|>$\sqrt{2}$,则点E在( )
 如图,已知长方形纸片ABCD在平面直角坐标系中,将该纸片沿AC对折,使得点B到达点E的位置,点A的坐标为(0,a),点B的坐标为(2,a),若∠BAC=67.5°,|a|>$\sqrt{2}$,则点E在( )
如图,已知长方形纸片ABCD在平面直角坐标系中,将该纸片沿AC对折,使得点B到达点E的位置,点A的坐标为(0,a),点B的坐标为(2,a),若∠BAC=67.5°,|a|>$\sqrt{2}$,则点E在( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
3.从一个多边形的任何一个顶点出发都只有6条对角线,则它的边数是( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
4.25的平方根是( )
| A. | 5 | B. | -5 | C. | ±5 | D. | 10 |
1.已知点A(0,4),B点在x轴上,AB与坐标轴围成的三角形面积为2,则B点坐标是( )
| A. | (1,0)或(-1,0) | B. | (1,0) | C. | (0,1)或(0,-1) | D. | (-1,0) |

 如图,在直角三角形ABC中,∠C=90°,AC=8,BC=6,设直线1⊥BC,且l从C向B平移,若CH=x,阴影部分面积为y,试求y关于x的函数关系式.
如图,在直角三角形ABC中,∠C=90°,AC=8,BC=6,设直线1⊥BC,且l从C向B平移,若CH=x,阴影部分面积为y,试求y关于x的函数关系式. 如图,点O为正方形ABCD的中心,BE平分∠DBC交DC于点E,延长BC到点F,使FC=EC,连结DF交BE的延长线于点H,连结OH交DC于点G,连结HC.则以下四个结论中:①OH∥BF,②GH=$\frac{1}{4}$BC,③OD=$\frac{1}{2}$BF,④∠CHF=45°.正确结论的个数为( )
如图,点O为正方形ABCD的中心,BE平分∠DBC交DC于点E,延长BC到点F,使FC=EC,连结DF交BE的延长线于点H,连结OH交DC于点G,连结HC.则以下四个结论中:①OH∥BF,②GH=$\frac{1}{4}$BC,③OD=$\frac{1}{2}$BF,④∠CHF=45°.正确结论的个数为( )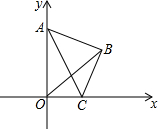 如图,在平面直角坐标系中,已知AB=BC,∠ABC=90°,若点A落在y轴上,点C落在x轴上,△ABC的形状始终不变,随着点C由原点O向x轴正半轴方向运动,点A沿y轴负半轴方向运动到终点O,在此次运动过程中,线段OB的长度变化情况是( )
如图,在平面直角坐标系中,已知AB=BC,∠ABC=90°,若点A落在y轴上,点C落在x轴上,△ABC的形状始终不变,随着点C由原点O向x轴正半轴方向运动,点A沿y轴负半轴方向运动到终点O,在此次运动过程中,线段OB的长度变化情况是( )