题目内容
3.在等腰三角形中,一边长为4,另一边长为7,求底边上的高.分析 分类讨论腰的长,若两腰长为7,则底边为5,根据勾股定理即可算出高;同理,若两腰长为5,则底边为7,根据勾股定理即可算出高,从而得出三角形的面积.
解答  解:(1)如图,AB=AC=7,BC=4,作底边上的高AD,
解:(1)如图,AB=AC=7,BC=4,作底边上的高AD,
∴BD=$\frac{1}{2}$BC=2,
根据勾股定理得,AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=$\sqrt{{7}^{2}-{2}^{2}}$=3$\sqrt{5}$,
(2)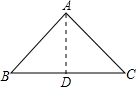 如图,AB=AC=4,BC=7,作底边上的高AD,
如图,AB=AC=4,BC=7,作底边上的高AD,
∴BD=$\frac{1}{2}$BC=$\frac{7}{2}$
根据勾股定理得,AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=$\sqrt{{4}^{2}-(\frac{7}{2})^{2}}$=$\frac{\sqrt{15}}{2}$.
点评 本题考查了等腰三角形的性质,勾股定理,属于基础题,关键是掌握等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.

练习册系列答案
相关题目
8.式子$\sqrt{1-2x}$在实数范围内有意义,则x的取值范围是( )
| A. | x≤$\frac{1}{2}$ | B. | x≥$\frac{1}{2}$ | C. | x≥-$\frac{1}{2}$ | D. | x≤-$\frac{1}{2}$ |
 如图,四边形ABCD是平行四边形,点M,N分别在DA,DN的延长线上,已知MN∥AC,求证:MQ=NP.
如图,四边形ABCD是平行四边形,点M,N分别在DA,DN的延长线上,已知MN∥AC,求证:MQ=NP. 如图,AB∥CD,AD与BC交于点O,如果∠B=40°,∠AOB=60°,求∠C、∠D的度数.
如图,AB∥CD,AD与BC交于点O,如果∠B=40°,∠AOB=60°,求∠C、∠D的度数.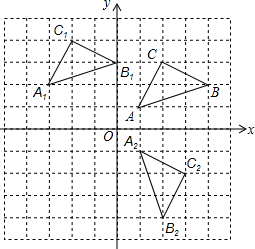 如图,方格纸中的每个小方格都是边长为1的单位小正方形,每个小正方形的顶点称为格点,△ABC的顶点都在格点上,建立平面直角坐标系后,点A、B、C的坐标分别为(1,1),(4,2),(2,3)
如图,方格纸中的每个小方格都是边长为1的单位小正方形,每个小正方形的顶点称为格点,△ABC的顶点都在格点上,建立平面直角坐标系后,点A、B、C的坐标分别为(1,1),(4,2),(2,3)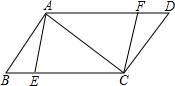 如图,在?ABCD中,AB=6,BC=10,对角线AC⊥AB,点E、F在BC、AD上,且BE=DF.
如图,在?ABCD中,AB=6,BC=10,对角线AC⊥AB,点E、F在BC、AD上,且BE=DF.