题目内容
18.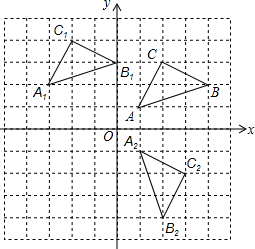 如图,方格纸中的每个小方格都是边长为1的单位小正方形,每个小正方形的顶点称为格点,△ABC的顶点都在格点上,建立平面直角坐标系后,点A、B、C的坐标分别为(1,1),(4,2),(2,3)
如图,方格纸中的每个小方格都是边长为1的单位小正方形,每个小正方形的顶点称为格点,△ABC的顶点都在格点上,建立平面直角坐标系后,点A、B、C的坐标分别为(1,1),(4,2),(2,3)(1)画出△ABC向左平移4个单位,再向上平移1个单位后得到的△A1B1C1;
(2)画出△ABC绕点O顺时针旋转90°后的△A2B2C2,并求出点A的运动路程.
分析 (1)利用平移的性质和网格特征画出点A、B、C的对应点A1、B1、C1即可得到△A1B1C1;
(2)利用网格特点和旋转的性质画出点A、B、C的对应点A2、B2、C2即可得到△A2B2C2,由于点A运动的路径为以O点为圆心,OA为半径,圆心角为90°的弧,则利用弧长公式计算即可.
解答 解:(1)如图,△A1B1C1为所求;
(2)如图,△A2B2C2为所求,
OA=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,
点A的运动路程长=$\frac{90•π•\sqrt{2}}{180}$=$\frac{\sqrt{2}π}{2}$.
点评 本题考查了作图-旋转变换法:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了平移变换.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目
6.某学校为七年级600名新生定做校服,校服型号有小号、中号、大号、特大号四种,随机抽取了100名学生调查他们的身高,得到身高(单位:厘米)频数分布表如下:
(1)全校应定做中号校服多少套?
(2)估计全校七年级学生的平均数身高是多少?
| 型号 | 身高(x/cm) | 人数(频数) |
| 小号 | 145≤x<155 | 22 |
| 中号 | 155≤x<165 | 45 |
| 大号 | 165≤x<175 | 28 |
| 特大号 | 175≤x<185 | 5 |
(2)估计全校七年级学生的平均数身高是多少?
 ,15不小心被墨汁涂抹了一个,只记得这组数的中位数与平均数相等,那么这组数据的中位数是20或17.5.
,15不小心被墨汁涂抹了一个,只记得这组数的中位数与平均数相等,那么这组数据的中位数是20或17.5.