题目内容
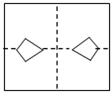
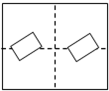
12.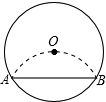 如图将半径为2cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长为( )
如图将半径为2cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长为( )| A. | 2cm | B. | $\sqrt{3}$cm | C. | 2$\sqrt{5}$cm | D. | 2$\sqrt{3}$cm |
分析 通过作辅助线,过点O作OD⊥AB交AB于点D,根据折叠的性质可知OA=2OD,根据勾股定理可将AD的长求出,通过垂径定理可求出AB的长.
解答  解:过点O作OD⊥AB交AB于点D,连接OA,
解:过点O作OD⊥AB交AB于点D,连接OA,
∵OA=2OD=2cm,
∴AD=$\sqrt{O{A}^{2}-O{D}^{2}}$=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$(cm),
∵OD⊥AB,
∴AB=2AD=2$\sqrt{3}$cm.
故选:D.
点评 本题考查了垂径定理和勾股定理的运用,正确应用勾股定理是解题关键.

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
20.等腰三角形一个角等于70°,则底角为( )
| A. | 70°或40° | B. | 40°或55° | C. | 55°或70° | D. | 70° |
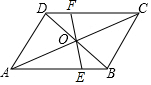 如图所示,在?ABCD中,EF过对角线AC,BD的交点O,若FC=3DF;S△BOE=2,那么,?ABCD 的面积为32.
如图所示,在?ABCD中,EF过对角线AC,BD的交点O,若FC=3DF;S△BOE=2,那么,?ABCD 的面积为32.
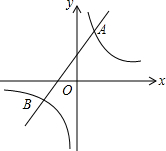 如图,一次函数y=k1x+b与反比例函数y=$\frac{{k}_{2}}{x}$的图象交于A(2,m),B(-3,-2)两点.
如图,一次函数y=k1x+b与反比例函数y=$\frac{{k}_{2}}{x}$的图象交于A(2,m),B(-3,-2)两点. 如图,计划在河边建一水厂,可过C点作CD⊥AB于D点.在D点建水厂,可使水厂到村庄C的路程最短,这样设计的依据是垂线段最短.
如图,计划在河边建一水厂,可过C点作CD⊥AB于D点.在D点建水厂,可使水厂到村庄C的路程最短,这样设计的依据是垂线段最短.