题目内容
7.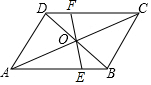 如图所示,在?ABCD中,EF过对角线AC,BD的交点O,若FC=3DF;S△BOE=2,那么,?ABCD 的面积为32.
如图所示,在?ABCD中,EF过对角线AC,BD的交点O,若FC=3DF;S△BOE=2,那么,?ABCD 的面积为32.
分析 由四边形ABCD是平行四边形,得出∠FDO=∠EBO、OD=OB,由ASA证得△FDO≌△EBO,得出S△DOF=S△BOE,求出S△COD=8即可得出结果.
解答 解:∵四边形ABCD是平行四边形,
∴∠FDO=∠EBO,OD=OB,
在△FDO和△EBO中,$\left\{\begin{array}{l}{∠FDO=∠EBO}\\{OD=OB}\\{∠FOD=∠EOB}\end{array}\right.$,
∴△FDO≌△EBO(ASA),
∴S△DOF=S△BOE,
∵S△BOE=2,
∴S△DOF=2,
∵FC=3DF,
∴S△COF=6,
∴S△COD=8,
∴?ABCD 的面积=4S△COD=4×8=32,
故答案为:32.
点评 本题主要考查了平行四边形的性质、全等三角形的判定与性质、三角形面积计算、平行四边形面积的计算等知识,熟练掌握全等三角形的面积相等与等高三角形面积计算是解决问题的关键.

练习册系列答案
相关题目
2. 如图,在?ABCD中,对角线AC、BD相交于点O,则下列式子不正确的是( )
如图,在?ABCD中,对角线AC、BD相交于点O,则下列式子不正确的是( )
 如图,在?ABCD中,对角线AC、BD相交于点O,则下列式子不正确的是( )
如图,在?ABCD中,对角线AC、BD相交于点O,则下列式子不正确的是( )| A. | BO=OD | B. | AB=CD | C. | ∠BAD=∠BCD | D. | AC=BD |
12.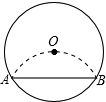 如图将半径为2cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长为( )
如图将半径为2cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长为( )
 如图将半径为2cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长为( )
如图将半径为2cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长为( )| A. | 2cm | B. | $\sqrt{3}$cm | C. | 2$\sqrt{5}$cm | D. | 2$\sqrt{3}$cm |
18. 下面是一组同学做“抛掷质地均匀的硬币试验”获得的数据.
下面是一组同学做“抛掷质地均匀的硬币试验”获得的数据.
(1)填写表中的空格;
(2)画出折线统计图;
(3)抛掷质地均匀的硬币,正面朝上的概率的估计值是多少?
 下面是一组同学做“抛掷质地均匀的硬币试验”获得的数据.
下面是一组同学做“抛掷质地均匀的硬币试验”获得的数据.| 抛掷次数 | 100 | 200 | 300 | 400 | 500 |
| 正面朝上的 频数m | 51 | 98 | 153 | 200 | 250 |
| 正面朝上的 频率mn | 0.51 | 0.49 | 0.51 | 0.50 | 0.51 |
(2)画出折线统计图;
(3)抛掷质地均匀的硬币,正面朝上的概率的估计值是多少?
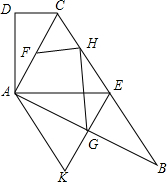 如图,在四边形ABCD中,AC平分∠BCD,AC2=CD•BC,E是BC的中点,AC⊥AB.
如图,在四边形ABCD中,AC平分∠BCD,AC2=CD•BC,E是BC的中点,AC⊥AB.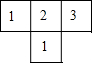 如图是由几个大小相同的小正方体搭成的几何体的俯视图,小正方体中的数字表示该位置小正方体的个数,则该几何体的正视图是( )
如图是由几个大小相同的小正方体搭成的几何体的俯视图,小正方体中的数字表示该位置小正方体的个数,则该几何体的正视图是( )