题目内容
18.P1(x1,y1),P2(x2,y2)是函数y=$\frac{1}{2}$x图象上的两点,则下列判断中正确的是( )| A. | y1>y2 | B. | y1<y2 | C. | 当x1<x2时,y1>y2 | D. | 当x1<x2时,y1<y2 |
分析 根据正比例函数的性质进行判断正确选项即可.
解答 解:∵$\frac{1}{2}$>0,
∴对于函数y=$\frac{1}{2}$x,y随x的增大而增大,
∴当x1<x2时,y1<y2,
故选D.
点评 本题考查了正比例函数图象的性质:它是经过原点的一条直线.当k>0时,图象经过一、三象限,y随x的增大而增大;当k<0时,图象经过二、四象限,y随x的增大而减小.

练习册系列答案
相关题目
13.若关于x的不等式组$\left\{\begin{array}{l}{x<2}\\{x-a≥0}\end{array}\right.$的整数解共有5个,则a的取值范围是( )
| A. | -4<a≤-3 | B. | -4≤a<-3 | C. | -4≤a≤-3 | D. | -4<a<-3 |
10.直线y=-$\frac{2}{3}$x-3与直线y=a(a为常数)的交点在第四象限,则a的值可能是( )
| A. | -2 | B. | 2 | C. | -4 | D. | 4 |
8.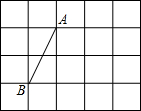 如图,A、B两点均在由小正方形组成的网格格点上,若C点也在格点上,且△ABC是等腰直角三角形,则符合条件的C点的个数有( )
如图,A、B两点均在由小正方形组成的网格格点上,若C点也在格点上,且△ABC是等腰直角三角形,则符合条件的C点的个数有( )
 如图,A、B两点均在由小正方形组成的网格格点上,若C点也在格点上,且△ABC是等腰直角三角形,则符合条件的C点的个数有( )
如图,A、B两点均在由小正方形组成的网格格点上,若C点也在格点上,且△ABC是等腰直角三角形,则符合条件的C点的个数有( )| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
 如图,一个圆锥的底面直径BC=1.4米,AB=2.5米,那么圆锥的高AO=2.4米.
如图,一个圆锥的底面直径BC=1.4米,AB=2.5米,那么圆锥的高AO=2.4米.
 如图所示,直线AC∥BD,AO、BO分别是∠BAC、∠ABD的平分线,那么∠BAO+∠ABO=90°.
如图所示,直线AC∥BD,AO、BO分别是∠BAC、∠ABD的平分线,那么∠BAO+∠ABO=90°.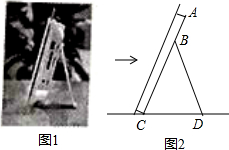 如图1是小红同学书桌上的一个电子相框,将其侧面抽象为如图2所示的几何图形,已知BC=BD=18cm,∠CBD=40°,则点B到CD的距离为16.9cm(用科学计算器计算.参考数据sin20°≈0.342,cos20°≈0.940,sin40°≈0.643,cos40°≈0.766,结果精确到0.1cm).
如图1是小红同学书桌上的一个电子相框,将其侧面抽象为如图2所示的几何图形,已知BC=BD=18cm,∠CBD=40°,则点B到CD的距离为16.9cm(用科学计算器计算.参考数据sin20°≈0.342,cos20°≈0.940,sin40°≈0.643,cos40°≈0.766,结果精确到0.1cm).