题目内容
10.直线y=-$\frac{2}{3}$x-3与直线y=a(a为常数)的交点在第四象限,则a的值可能是( )| A. | -2 | B. | 2 | C. | -4 | D. | 4 |
分析 先求出直线y=-$\frac{2}{3}$x-3与y轴的交点,得到a<-3,根据题意选择即可.
解答 解:∵直线y=-$\frac{2}{3}$x-3与y轴的交点为(0,-3),
而直线y=-$\frac{2}{3}$x-3与直线y=a(a为常数)的交点在第四象限,
∴a<-3.
故选:C.
点评 本题考查了两直线相交或平行问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解;若两条直线是平行的关系,那么它们的自变量系数相同,即k值相同.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.P1(x1,y1),P2(x2,y2)是函数y=$\frac{1}{2}$x图象上的两点,则下列判断中正确的是( )
| A. | y1>y2 | B. | y1<y2 | C. | 当x1<x2时,y1>y2 | D. | 当x1<x2时,y1<y2 |
2.下列各整式中,次数为3次的单项式是( )
| A. | xy2 | B. | xy3 | C. | x+y2 | D. | x+y3 |

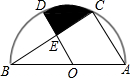 如图,半圆O中,AB为直径,AB=4,C、D为半圆上两点,四边形OACD为菱形,连接BC交OD于点E,则阴影部分面积为$\frac{2}{3}$π-$\frac{\sqrt{3}}{2}$.
如图,半圆O中,AB为直径,AB=4,C、D为半圆上两点,四边形OACD为菱形,连接BC交OD于点E,则阴影部分面积为$\frac{2}{3}$π-$\frac{\sqrt{3}}{2}$.