Question

3．（1）如图①，∠CEF=90°，点B在射线EF上，AB∥CD．若∠ABE=130°，求∠C的度数；
（2）如图②，把“∠CEF=90°”改为“∠CEF=120°”，AB∥CD．猜想∠ABE与∠C的数量关系，并说明理由；（3）如图③，在（2）的条件下，作GC⊥CE，垂足为C，反向延长CD至H，若∠GCH=θ，则∠ABE=150°-θ（请用含θ的式子表示）．

Answer 1

分析 （1）过E作EK∥AB，则∠ABE+∠1=180°，根据AB∥CD，EK∥AB，即可得到EK∥CD，再根据平行线的性质，即可得到∠C的度数；
（2）过E作EK∥AB，则∠ABE+∠1=180°，根据AB∥CD，EK∥AB，即可得到EK∥CD，再根据平行线的性质，即可得到180°-∠ABE+∠C=120°，据此可得∠ABE与∠C的数量关系
（3）过E作EK∥AB，则∠ABE+∠KEB=180°，再根据AB∥CD，EK∥AB，可得EK∥CD，根据∠ABE+∠BEC+∠DCE=360°，可得∠ABE+120°+90°+θ=360°，进而得到∠ABE=150°-θ．

解答 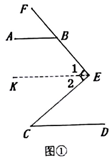解：（1）如图①，过E作EK∥AB，则∠ABE+∠1=180°，
∴∠1=180°-∠ABE=50°，
∵∠CEF=90°，
∴∠2=90°-∠1=40°，
∵AB∥CD，EK∥AB，
∴EK∥CD，
∴∠C=∠2=40°；

（2）∠ABE-∠C=60°，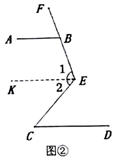
理由：如图②，过E作EK∥AB，则∠ABE+∠1=180°，
∴∠1=180°-∠ABE，
∵AB∥CD，EK∥AB，
∴EK∥CD，
∴∠C=∠2，
∵∠CEF=∠1+∠2=120°，即180°-∠ABE+∠C=120°，
∴∠ABE-∠C=180°-120°=60°；

（3）如图③，过E作EK∥AB，则∠ABE+∠KEB=180°，
∵AB∥CD，EK∥AB，
∴EK∥CD，
∴∠DCE+∠KEC=180°，
∴∠ABE+∠BEC+∠DCE=360°，
又∵GC⊥CE，∠GCH=θ，∠CEF=120°，
∴∠ABE+120°+90°+θ=360°，
∴∠ABE=150°-θ．
故答案为：150°-θ．

点评 本题主要考查了平行线的性质，解题时注意：两直线平行，同旁内角互补；两直线平行，内错角相等．解决问题的关键是作辅助线构造同旁内角以及内错角．