题目内容
20. 如图,AB是⊙O的直径,E为弦AC的延长线上一点,DE与⊙O相切于点D,且DE⊥AC,连结OD,若AB=10,AC=6,求DE的长.
如图,AB是⊙O的直径,E为弦AC的延长线上一点,DE与⊙O相切于点D,且DE⊥AC,连结OD,若AB=10,AC=6,求DE的长.
分析 连结BC,如图,BC与OD相交于点F,利用圆周角定理得到BC⊥AE,则BC∥DE,再利用切线的性质得到OD⊥DE,接着利用垂径定理得到CF=$\frac{1}{2}$BC,接下来判定四边形CEDF是矩形得到DE=CF=$\frac{1}{2}$BC,然后利用勾股定理计算出BC,从而得到CF和DE的长.
解答 解:连结BC,如图,BC与OD相交于点F,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴BC⊥AE,
又∵DE⊥AC,
∴BC∥DE,
∵DE是⊙O的切线,
∴OD⊥DE,
∴OD⊥BC,
∴CF=$\frac{1}{2}$BC,
∵BC⊥AE,DE⊥AC,DE⊥AC,
∴四边形CEDF是矩形.
∴DE=CF=$\frac{1}{2}$BC,
在Rt△ACB中,∠ACB=90°,
∴BC=$\sqrt{1{0}^{2}-{6}^{2}}$=8,
∴CF=4,
∴DE=4.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了垂径定理和勾股定理.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 为了对一棵倾斜的古杉树AB进行保护,需测量其长度.如图,在地面上选取一点C,测得∠ACB=45°,AC=21m,∠BAC=53°,求这颗古杉树AB的长度.
为了对一棵倾斜的古杉树AB进行保护,需测量其长度.如图,在地面上选取一点C,测得∠ACB=45°,AC=21m,∠BAC=53°,求这颗古杉树AB的长度. 如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D,AD交⊙O于点E.
如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D,AD交⊙O于点E.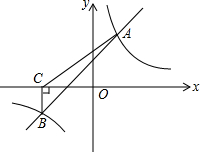 如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(2,4)、B(-4,n)两点.
如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(2,4)、B(-4,n)两点. 某商店试销一种新商品,该商品的进价为40元/件,经过一段时间的试销发现,每月的销售量会因售价在40~70元之间的调整而不同.当售价在40~50元时,每月销售量都为60件;当售价在50~70元时,每月销售量与售价的关系如图所示,令每月销售量为y件,售价为x元/件,每月的总利润为Q元.
某商店试销一种新商品,该商品的进价为40元/件,经过一段时间的试销发现,每月的销售量会因售价在40~70元之间的调整而不同.当售价在40~50元时,每月销售量都为60件;当售价在50~70元时,每月销售量与售价的关系如图所示,令每月销售量为y件,售价为x元/件,每月的总利润为Q元. 如图,在?ABCD中,AE=CG,求证:GF=HE.
如图,在?ABCD中,AE=CG,求证:GF=HE.