题目内容
11.等腰三角形两边长为acm,bcm,第三边为8cm,且a,b是方程x2-12x+n-1=0的两根,则n的值为37或33.分析 分a、b为腰以及a(或b)为底两种情况考虑:当a、b为腰时,根据根的判别式△=148-4n=0可求出n值,再解出a、b的值,利用三角形三边关系可确定此种情况符合题意;当a(或b)为底时,将x=8代入原方程可求出n值,进而求出a、b值,利用三角形三边关系可确定此种情况符合题意.综上即可得出结论.
解答 解:当a、b为腰时,方程x2-12x+n-1=0有两个相等的实数根,
∴△=(-12)2-4(n-1)=148-4n=0,
解得:n=37,
此时a=b=6.
∵6、6、8能组成三角形,
∴此情况符合题意;
当a(或b)为底时,将x=8代入原方程,
得:82-12×8+n-1=0,
解得:n=33,
此时a=4,b=8(或a=8,b=4).
∵8、8、4能组成三角形,
∴此情况符合题意.
综上所述:n的值为37或33.
故答案为:37或33.
点评 本题考查了根的判别式、一元二次方程的解、三角形三边关系以及等腰三角形的性质,分a、b为腰以及a(或b)为底两种情况求n值是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.2016年,义乌市经济总体平稳,全年实现地区生产总值1118亿元.将1118亿元用科学记数法表示应为(单位:元)( )
| A. | 1.118×103 | B. | 1.118×1010 | C. | 1.118×1011 | D. | 1.118×1012 |
 如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D,AD交⊙O于点E.
如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D,AD交⊙O于点E. 如图,在?ABCD中,AE=CG,求证:GF=HE.
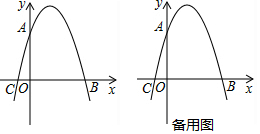
如图,在?ABCD中,AE=CG,求证:GF=HE. 如图,在平面直角坐标系中,抛物线y=-x2+4x与x轴交于点A,点M是x轴上方抛物线上一点,过点M作MP⊥x轴于点P,以MP为对角线作矩形MNPQ,连结NQ,则对角线NQ的最大值为4.
如图,在平面直角坐标系中,抛物线y=-x2+4x与x轴交于点A,点M是x轴上方抛物线上一点,过点M作MP⊥x轴于点P,以MP为对角线作矩形MNPQ,连结NQ,则对角线NQ的最大值为4. 如图,E是?ABCD边DC上一点,请你只用一把没有刻度的直尺,在AB边上确定一点F,使得BF=DE,画出示意图,并简要说明画图过程.
如图,E是?ABCD边DC上一点,请你只用一把没有刻度的直尺,在AB边上确定一点F,使得BF=DE,画出示意图,并简要说明画图过程.
 如图,已知线段AB,请用直尺(不带刻度的直尺)和圆规作一个以AB为腰、底角等于30°的等腰△ABC.
如图,已知线段AB,请用直尺(不带刻度的直尺)和圆规作一个以AB为腰、底角等于30°的等腰△ABC.