题目内容
如图，△ABC中，DE∥BC，EF∥AB，AD：BD=3：2，FC=2，AC=6，求DE和CE的长．考点：平行线分线段成比例
专题：
分析：由平行可得
=
，
=
，且AE=AC-EC，BC=CF+BF=CF+DE，代入可求得DE和CE．
| DE |
| BC |
| AD |
| AB |
| AD |
| DB |
| AE |
| EC |
解答：解：
∵DE∥BC，
∴
=
=
，
∵AC=6，
∴AE=AC-CE=6-CE，
∴
=
，解得CE=2.4，
∵EF∥AB，
∴四边形BDEF是平行四边形，
∴DE=BF，
∴BC=DE+CF=DE+2，
∵AD：BD=3：2，
∴AD：AB=3：5，
∴
=
=
，
即
=
，解得DE=3．
∵DE∥BC，
∴
| AD |
| DB |
| AE |
| EC |
| 3 |
| 2 |
∵AC=6，
∴AE=AC-CE=6-CE，
∴
| 6-CE |
| CE |
| 3 |
| 2 |
∵EF∥AB，
∴四边形BDEF是平行四边形，
∴DE=BF，
∴BC=DE+CF=DE+2，
∵AD：BD=3：2，
∴AD：AB=3：5，
∴
| DE |
| BC |
| AD |
| AB |
| 3 |
| 5 |
即
| DE |
| DE+2 |
| 3 |
| 5 |
点评：本题主要考查平行线分线段成比例，掌握平行线分线段所得线段对应成比例是解题的关键，注意方程思想的应用．
练习册系列答案
相关题目
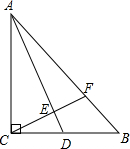如图，已知在△ABC中，∠ACB=90°，AC=BC，AD是BC边上的中线，CE⊥AD于E，CE延长线交AB于F．求：